Асимметрия и эксцесс эмпирического распределения определяются, соответственно, равенствами:  ,
,  ; (10.1)
; (10.1)
здесь  – выборочное среднее квадратическое отклонение;
– выборочное среднее квадратическое отклонение;
 и
и  – центральные эмпирические моменты третьего и четвертого порядков:
– центральные эмпирические моменты третьего и четвертого порядков:  ,
,  . (28)
. (28)
Эти моменты в случае равноотстоящих вариант с шагом  (шаг равен разности между любыми двумя соседними вариантами) удобно вычислять по формулам:
(шаг равен разности между любыми двумя соседними вариантами) удобно вычислять по формулам:
 ,
,  , (29)
, (29)
где  – условные моменты
– условные моменты 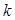 -го порядка;
-го порядка;  – условные варианты.
– условные варианты.
Здесь 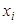 – первоначальные варианты;
– первоначальные варианты;  – ложный нуль, то есть варианта, имеющая наибольшую частоту (либо любая варианта, расположенная примерно в середине вариационного ряда).
– ложный нуль, то есть варианта, имеющая наибольшую частоту (либо любая варианта, расположенная примерно в середине вариационного ряда).
Итак, для отыскания асимметрии и эксцесса необходимо вычислить условные моменты, что можно сделать методом произведений или методом сумм.

 ,
,  ; (10.1)
; (10.1) – выборочное среднее квадратическое отклонение;
– выборочное среднее квадратическое отклонение; и
и  – центральные эмпирические моменты третьего и четвертого порядков:
– центральные эмпирические моменты третьего и четвертого порядков:  ,
,  . (28)
. (28) (шаг равен разности между любыми двумя соседними вариантами) удобно вычислять по формулам:
(шаг равен разности между любыми двумя соседними вариантами) удобно вычислять по формулам: ,
,  , (29)
, (29) – условные моменты
– условные моменты 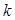 -го порядка;
-го порядка;  – условные варианты.
– условные варианты.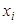 – первоначальные варианты;
– первоначальные варианты;  – ложный нуль, то есть варианта, имеющая наибольшую частоту (либо любая варианта, расположенная примерно в середине вариационного ряда).
– ложный нуль, то есть варианта, имеющая наибольшую частоту (либо любая варианта, расположенная примерно в середине вариационного ряда).


