Пусть 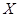 – дискретная случайная величина, которая в результате
– дискретная случайная величина, которая в результате 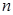 опытов приняла возможные значения
опытов приняла возможные значения 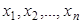 . Допустим, что вид закона распределения величины
. Допустим, что вид закона распределения величины 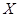 задан, но неизвестен параметр
задан, но неизвестен параметр  , которым определяется этот закон; требуется найти его точечную оценку
, которым определяется этот закон; требуется найти его точечную оценку  [4].
[4].
Обозначим вероятность того, что в результате испытания величина 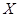 примет значение
примет значение 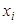 через
через  .
.
Функцией правдоподобия дискретной случайной величины 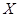 называют функцию аргумента
называют функцию аргумента  :
:
 . (15)
. (15)
Оценкой наибольшего правдоподобия параметра  называют такое его значение
называют такое его значение  , при котором функция правдоподобия достигает максимума.
, при котором функция правдоподобия достигает максимума.
Функции  и
и  достигают максимума при одном и том же значении
достигают максимума при одном и том же значении  , поэтому вместо отыскания максимума функции
, поэтому вместо отыскания максимума функции  ищут, что удобнее, максимум функции
ищут, что удобнее, максимум функции  .
.
Логарифмической функцией правдоподобия называют функцию  .
.
Точку максимума функции  аргумента
аргумента  можно искать, например, так:
можно искать, например, так:
1. Найти производную  .
.
2. Приравнять производную нулю и найти критическую точку  – корень полученного уравнения (его называют уравнением правдоподобия).
– корень полученного уравнения (его называют уравнением правдоподобия).
3. Найти вторую производную  ; если вторая производная при
; если вторая производная при  отрицательная, то
отрицательная, то  – точка максимума.
– точка максимума.
Найденную точку максимума  принимают в качестве оценки наибольшего правдоподобия параметра
принимают в качестве оценки наибольшего правдоподобия параметра  .
.
Для получения последовательности возможных значений дискретной случайной величины, зная ее закон распределения, то есть для разыгрывания дискретной случайной величины, в приложении 9 приведены значения равномерно распределенных чисел.

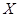 – дискретная случайная величина, которая в результате
– дискретная случайная величина, которая в результате 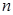 опытов приняла возможные значения
опытов приняла возможные значения 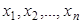 . Допустим, что вид закона распределения величины
. Допустим, что вид закона распределения величины  , которым определяется этот закон; требуется найти его точечную оценку
, которым определяется этот закон; требуется найти его точечную оценку  [4].
[4].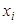 через
через  .
. . (15)
. (15) , при котором функция правдоподобия достигает максимума.
, при котором функция правдоподобия достигает максимума. и
и  достигают максимума при одном и том же значении
достигают максимума при одном и том же значении  .
. ; если вторая производная при
; если вторая производная при  отрицательная, то
отрицательная, то 


