Метод моментов
Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка. Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (12) относительно неизвестного параметра, тем самым получим его точечную оценку.
Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: Учитывая, что
Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (5.2) относительно неизвестных параметров, тем самым получим их точечные оценки. Разумеется, для вычисления выборочной средней Пример. Случайная величина
где
Найти методом моментов по выборке Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравняем начальный теоретический момент первого порядка
Приняв во внимание, что Итак, точечной оценкой параметра
Пример. Найти методом моментов по выборке
Решение. Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка
Учитывая, что
Математическое ожидание и дисперсия гамма-распределения соответственно равны
Решив эту систему, окончательно получим искомые точечные оценки неизвестных параметров:
|

 . Учитывая, что
. Учитывая, что 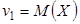 и
и 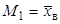 , получим
, получим  . (12)
. (12)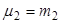 .
.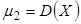 ,
, 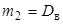 , имеем
, имеем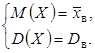 (13)
(13)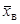 и выборочной дисперсии
и выборочной дисперсии 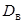 надо располагать выборкой
надо располагать выборкой 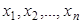 .
.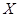 распределена по закону Пуассона
распределена по закону Пуассона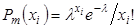 ,
,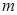 – число испытаний, произведенных в одном опыте;
– число испытаний, произведенных в одном опыте;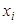 – число появлений события в
– число появлений события в 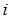 -м опыте.
-м опыте.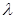 , определяющего распределение Пуассона.
, определяющего распределение Пуассона.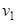 начальному эмпирическому моменту первого порядка
начальному эмпирическому моменту первого порядка 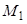 :
: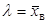 .
.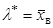 .
. и
и 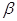 гамма-распределения, плотность которого
гамма-распределения, плотность которого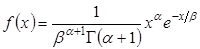
 .
.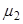 центральному эмпирическому моменту второго порядка
центральному эмпирическому моменту второго порядка  :
: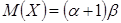 ,
,  , поэтому (143) можно записать в виде
, поэтому (143) можно записать в виде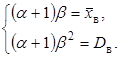
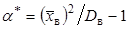 ,
, 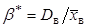 .
.


