Полигон и гистограмма
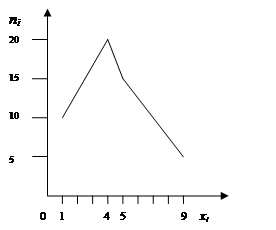
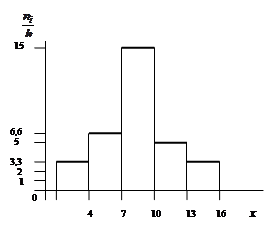
§ 3.1. Дискретное распределение признака Полигоном частот называют ломаную, отрезки которой соединяют точки Полигоном относительных частот называют ломаную, отрезки которой соединяют точки § 3.2. Непрерывное распределение признака При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины Пример. Построить полигон частот по данному распределению выборки:
Решение. Отложим на оси абсцисс варианты
Рис.2. Полигон частот Рис.3. Гистограмма частот
|
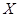
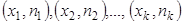, где 
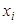– варианты выборки и 
– соответствующие им частоты.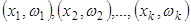
, где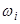 
соответствующие им относительные частоты.
и находят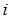 
-й интервал.
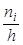(плотность относительной частоты). Площадь частичного 
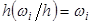– относительной частоте вариант, попавших в 
.
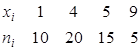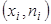отрезками прямых, получим искомый полигон частот (рис.2).
