Точечные оценки
Статистической оценкой Точечной называют статистическую оценку, которая определяется одним числом Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру. Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя где Замечание 1. Если первоначальные варианты Тогда Смещенной оценкой генеральной дисперсии служит выборочная дисперсия
эта оценка является смещенной, так как Более удобна формула Замечание 2. Если первоначальные варианты Тогда Замечание 3. Если первоначальные варианты являются десятичными дробями с надо разделить ее на
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия Более удобная формула В условных вариантах она имеет вид причем если Замечание 4. При большом числе данных используют метод произведений или метод сумм. Пример. Из генеральной совокупности извлечена выборка объема Найти несмещенную оценку генеральной средней. Решение. Несмещенной оценкой генеральной средней является выборочная средняя
Пример. Найти выборочную среднюю по данному распределению выборки объема Решение. Первоначальные варианты – большие числа, поэтому перейдем к условным вариантам
Найдем искомую выборочную среднюю:
Пример. Найти выборочную дисперсию по данному распределению выборки объема Решение. Варианты – сравнительно большие числа, поэтому перейдем к условным вариантам Найдем искомую выборочную дисперсию:
|

 неизвестного параметра
неизвестного параметра  теоретического распределения называют функцию
теоретического распределения называют функцию 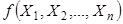 от наблюдаемых случайных величин
от наблюдаемых случайных величин 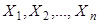 .
.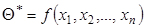 , где
, где 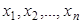 – результаты
– результаты 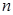 наблюдений над количественным признаком
наблюдений над количественным признаком 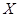 (выборка).
(выборка).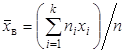 , (2)
, (2)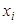 – варианта выборки;
– варианта выборки;  – частота варианты
– частота варианты 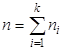 – объем выборки.
– объем выборки. , то есть перейти к условным вариантам
, то есть перейти к условным вариантам 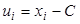 (в качестве
(в качестве 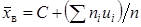 . (3)
. (3)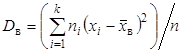 ; (4)
; (4)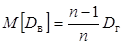 . (5)
. (5)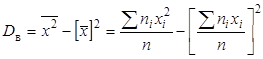 . (6)
. (6)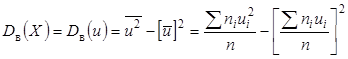 . (7)
. (7)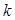 десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число
десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные варианты на постоянное число 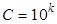 , то есть переходят к условным вариантам
, то есть переходят к условным вариантам 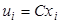 . При этом, дисперсия увеличивается в
. При этом, дисперсия увеличивается в 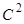 раз, поэтому, найдя дисперсию условных вариант,
раз, поэтому, найдя дисперсию условных вариант,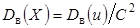 . (8)
. (8)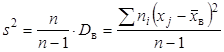 . (9)
. (9)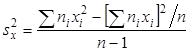 . (10)
. (10)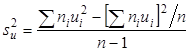 , (11)
, (11)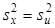 ; если
; если 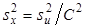 .
.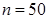 :
: 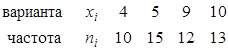 .
.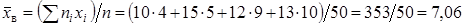 .
.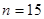 :
: 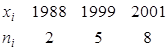 .
.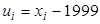 . В итоге получим распределение условных вариант:
. В итоге получим распределение условных вариант: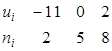 .
.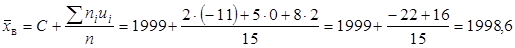 .
.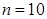 :
: 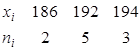 .
.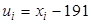 (мы вычли из вариант число
(мы вычли из вариант число 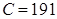 , близкое к выборочной средней). В итоге получим распределение условных вариант:
, близкое к выборочной средней). В итоге получим распределение условных вариант: 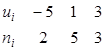 .
.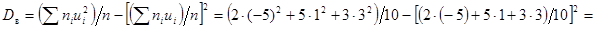
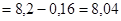 .
.


