Пусть 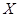 – непрерывная случайная величина, которая в результате
– непрерывная случайная величина, которая в результате 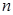 испытаний приняла значения
испытаний приняла значения 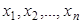 . Допустим, что вид плоскости распределения – функции
. Допустим, что вид плоскости распределения – функции  – задан, но неизвестен параметр
– задан, но неизвестен параметр  , которым определяется эта функция.
, которым определяется эта функция.
Функцией правдоподобия непрерывной случайной величины 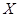 называют функцию аргумента
называют функцию аргумента  :
:
 . (16)
. (16)
Оценку наибольшего правдоподобия неизвестного параметра распределения случайной величины ищут так же, как в случае дискретной случайной величины.
Если плотность распределения  непрерывной случайной величины определяется двумя неизвестными параметрами
непрерывной случайной величины определяется двумя неизвестными параметрами  и
и 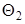 , то функция правдоподобия есть функция двух независимых аргументов
, то функция правдоподобия есть функция двух независимых аргументов  и
и 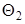 :
:
 .
.
Далее находят логарифмическую функцию правдоподобия и для отыскания ее максимума составляют и решают систему
 (17)
(17)
Пример. Найти методом наибольшего правдоподобия точечную оценку неизвестного параметра  (вероятность появления события в одном испытании) биноминального распределения
(вероятность появления события в одном испытании) биноминального распределения  ,
,
где 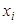 – число появлений события в
– число появлений события в 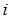 -м опыте;
-м опыте;
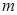 – количество испытаний в одном опыте;
– количество испытаний в одном опыте;
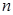 – число опытов.
– число опытов.
Решение. Составим функцию правдоподобия:  .
.
Учитывая, что  и
и  , получим
, получим
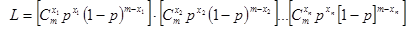
или 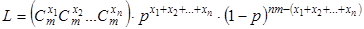 .
.
Напишем логарифмическую функцию правдоподобия:
 .
.
Найдем первую производную по  :
:
 .
.
Приравняв первую производную нулю и решив полученное уравнение, получим критическую точку  .
.
Найдем вторую производную по 
 .
.
Легко убедиться, что при  вторая производная отрицательна; следовательно, эта точка есть точка максимума и ее надо принять в качестве оценки наибольшего правдоподобия неизвестной вероятности
вторая производная отрицательна; следовательно, эта точка есть точка максимума и ее надо принять в качестве оценки наибольшего правдоподобия неизвестной вероятности  биноминального распределения:
биноминального распределения:  .
.
Очевидно, что если 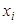 появлений события наблюдалось в
появлений события наблюдалось в  опытах, то
опытах, то
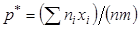 .
.
Пример. Найти методом наибольшего правдоподобия по выборке 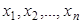 точечную оценку неизвестного параметра
точечную оценку неизвестного параметра 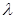 показательного распределения, плотность которого
показательного распределения, плотность которого  .
.
Решение. Составим функцию правдоподобия
 ,
,
учитывая, что  и, следовательно,
и, следовательно,  :
:
 .
.
Найдем логарифмическую функцию правдоподобия:
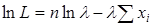 .
.
Найдем первую производную по 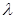 :
:  .
.
Запишем уравнение правдоподобия, для чего приравняем первую производную нулю:  . Найдем относительную точку, для чего решим полученное уравнение относительно
. Найдем относительную точку, для чего решим полученное уравнение относительно 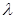 :
: 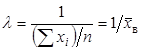 .
.
Найдем вторую производную по 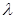 :
:  .
.
Легко видеть, что при  вторая производная отрицательна, следовательно, эта точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней:
вторая производная отрицательна, следовательно, эта точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней:  .
.

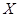 – непрерывная случайная величина, которая в результате
– непрерывная случайная величина, которая в результате 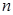 испытаний приняла значения
испытаний приняла значения 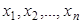 . Допустим, что вид плоскости распределения – функции
. Допустим, что вид плоскости распределения – функции  – задан, но неизвестен параметр
– задан, но неизвестен параметр  , которым определяется эта функция.
, которым определяется эта функция. . (16)
. (16) и
и 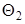 , то функция правдоподобия есть функция двух независимых аргументов
, то функция правдоподобия есть функция двух независимых аргументов  .
. (17)
(17) (вероятность появления события в одном испытании) биноминального распределения
(вероятность появления события в одном испытании) биноминального распределения  ,
,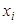 – число появлений события в
– число появлений события в 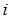 -м опыте;
-м опыте;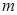 – количество испытаний в одном опыте;
– количество испытаний в одном опыте; .
. и
и  , получим
, получим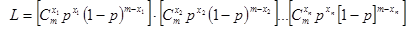
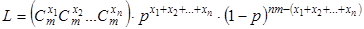 .
. .
. .
. .
. .
. .
. опытах, то
опытах, то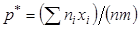 .
.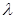 показательного распределения, плотность которого
показательного распределения, плотность которого  .
. ,
, и, следовательно,
и, следовательно,  :
: .
.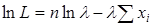 .
. .
. . Найдем относительную точку, для чего решим полученное уравнение относительно
. Найдем относительную точку, для чего решим полученное уравнение относительно 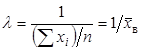 .
. .
. вторая производная отрицательна, следовательно, эта точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней:
вторая производная отрицательна, следовательно, эта точка есть точка максимума и, значит, в качестве оценки наибольшего правдоподобия надо принять величину, обратную выборочной средней:  .
.


