Метод сумм для вычисления выборочной средней и дисперсии
Пусть выборка задана в виде распределения равноотстоящих вариант и соответствующих им частот. В этом случае выборочные среднюю и дисперсию можно вычислить по формулам:
При использовании метода сумм условные моменты первого и второго порядков находят по формулам: где Таким образом, в конечном счете, надо вычислить числа Пример. Найти методом сумм выборочную среднюю и выборочную дисперсию по заданному распределению выборки объема
Решение. Составим расчетную табл. 9.1, для этого: 1) запишем варианты в первый столбец; 2) запишем частоты во второй столбец; сумму частот (100) поместим в нижнюю клетку столбца; 3) в качестве ложного нуля 4) в оставшихся незаполненными над нулем клетках третьего столбца (исключая самую верхнюю) запишем последовательно накопленные частоты: 3; 3+4=7; 7+8=15; 15+14=29; 29+20=49; сложив все накопленные частоты, получим число 5) аналогично заполняется четвертый столбец, причем суммируют частоты третьего столбца; сложив все накопленные частоты, расположенные над нулем, получим число Таблица 2
Найдем
Найдем условные моменты первого и второго порядков:
Вычислим искомые выборочную среднюю и выборочную дисперсию, учитывая, что шаг (разность между двумя соседними вариантами)
|

 ,
,  . (26)
. (26)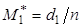 ,
, 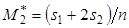 , (27)
, (27)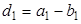 ,
, 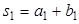 ,
, 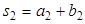 .
.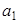 ,
, 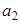 ,
, 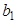 ,
, 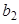 .
.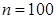 :
: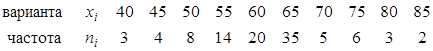 .
. выберем варианту (65), которая имеет наибольшую частоту (в качестве
выберем варианту (65), которая имеет наибольшую частоту (в качестве 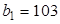 , которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты: 2; 2+3=5; 5+6=11; 11+5=16; сложив все накопленные частоты, получим число
, которое поместим в верхнюю клетку третьего столбца. В оставшихся незаполненными под нулем клетках третьего столбца (исключая самую нижнюю) запишем последовательно накопленные частоты: 2; 2+3=5; 5+6=11; 11+5=16; сложив все накопленные частоты, получим число 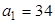 , которое поместим в нижнюю клетку третьего столбца;
, которое поместим в нижнюю клетку третьего столбца;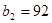 , которое поместим в верхнюю клетку четвертого столбца; сумма накопленных частот, расположенных под нулем, равна числу
, которое поместим в верхнюю клетку четвертого столбца; сумма накопленных частот, расположенных под нулем, равна числу 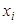

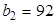
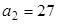
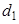 ,
, 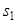 ,
, 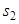 :
: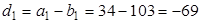 ;
; 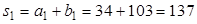 ;
;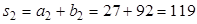 .
.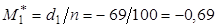 ,
,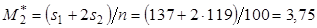 .
.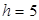 и ложный нуль
и ложный нуль 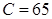 :
: 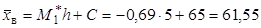 ;
;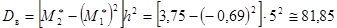 .
.


