Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью  покрывает заданный параметр.
покрывает заданный параметр.
1. Интервальной оценкой (с надежностью  ) математического ожидания
) математического ожидания  нормально распределенного количественного признака
нормально распределенного количественного признака 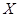 по выборочной средней
по выборочной средней 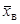 при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении  генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал
 , (18)
, (18)
где  – точность оценки;
– точность оценки;
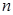 – объем выборки;
– объем выборки;
 – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  , при котором
, при котором  ; при неизвестном
; при неизвестном  (и объеме выборки
(и объеме выборки  )
)
 , (19)
, (19)
где  – «исправленное» выборочное среднее квадратическое отклонение,
– «исправленное» выборочное среднее квадратическое отклонение,  находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным 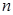 и
и  .
.
2. Интервальной оценкой (с надежностью  ) среднего квадратичекого отклонения
) среднего квадратичекого отклонения  нормально распределенного количественного признака
нормально распределенного количественного признака 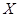 по «исправленному» выборочному среднему квадратическому отклонению
по «исправленному» выборочному среднему квадратическому отклонению  служит доверительный интервал
служит доверительный интервал
 (20)
(20)
где  находят по таблице приложения 4 с заданными
находят по таблице приложения 4 с заданными 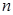 и
и  .
.
3. Интервальной оценкой (с надежностью  ) неизвестной вероятности
) неизвестной вероятности  биноминального распределения по относительной частоте
биноминального распределения по относительной частоте  служит доверительный интервал (с приближенными концами
служит доверительный интервал (с приближенными концами  и
и  )
)
 ,
,
где  (21)
(21)
где 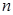 – общее число испытаний;
– общее число испытаний; 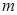 – число появлений события;
– число появлений события;  – относительная частота, равная отношению
– относительная частота, равная отношению  ;
;  – значение аргумента функции Лапласа (приложение 2), при котором
– значение аргумента функции Лапласа (приложение 2), при котором  (
( – заданная надежность).
– заданная надежность).
Замечание. При больших значениях 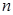 (порядка сотен) можно принять в качестве приближенных границ доверительного интервала
(порядка сотен) можно принять в качестве приближенных границ доверительного интервала
 ,
,  . (22)
. (22)
Пример. Найти доверительный интервал для оценки с надежностью 0, 975 неизвестного математического ожидания  нормально распределенного признака
нормально распределенного признака 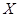 генеральной совокупности, если генеральное среднее квадратическое отклонение
генеральной совокупности, если генеральное среднее квадратическое отклонение  , выборочная средняя
, выборочная средняя  и объем выборки
и объем выборки 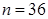 .
.
Решение. Требуется найти доверительный интервал
 . (23)
. (23)
Все величины, кроме  , известны. Найдем
, известны. Найдем  из соотношения
из соотношения  . По таблице приложения 1 находим
. По таблице приложения 1 находим  . Подставив
. Подставив  ,
,  ,
,  ,
, 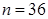 в (23), окончательно получим искомый доверительный интервал
в (23), окончательно получим искомый доверительный интервал  .
.
Пример. Найти минимальный объем выборки, при котором с надежностью 0, 95 точность оценки математического ожидания  генеральной совокупности по выборочной средней равна
генеральной совокупности по выборочной средней равна  , если известно среднее квадратическое отклонение
, если известно среднее квадратическое отклонение  нормально распределенной генеральной совокупности.
нормально распределенной генеральной совокупности.
Решение. Воспользуемся формулой, определяющей точность оценки математического ожидания генеральной совокупности по выборочной средней: 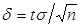 .
.
Отсюда  . (24)
. (24)
по условию, 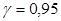 ; следовательно,
; следовательно,  . По таблице приложения 2 найдем
. По таблице приложения 2 найдем  . Подставив
. Подставив  ,
,  и
и  в (24), получим искомый объем выборки
в (24), получим искомый объем выборки  .
.
Пример. Произведено 15 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем «исправленное» среднее квадратическое отклонение  случайных ошибок измерений оказалось равным 0, 7. Найти точность прибора с надежностью 0, 99. Предполагается, что результаты измерений распределены нормально.
случайных ошибок измерений оказалось равным 0, 7. Найти точность прибора с надежностью 0, 99. Предполагается, что результаты измерений распределены нормально.
Решение. Точность прибора характеризуется средним квадратическом отклонением случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала, покрывающего  с заданной надежностью
с заданной надежностью  :
:
 . (25)
. (25)
По данным  и
и  по таблице приложения 4 найдем
по таблице приложения 4 найдем  . Подставив
. Подставив  ,
,  в соотношение (25), окончательно получим
в соотношение (25), окончательно получим  .
.

 покрывает заданный параметр.
покрывает заданный параметр. нормально распределенного количественного признака
нормально распределенного количественного признака 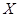 по выборочной средней
по выборочной средней 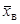 при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении  генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал , (18)
, (18) – точность оценки;
– точность оценки;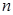 – объем выборки;
– объем выборки; – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  , при котором
, при котором  ; при неизвестном
; при неизвестном  )
) , (19)
, (19) – «исправленное» выборочное среднее квадратическое отклонение,
– «исправленное» выборочное среднее квадратическое отклонение,  находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным  (20)
(20) находят по таблице приложения 4 с заданными
находят по таблице приложения 4 с заданными  биноминального распределения по относительной частоте
биноминального распределения по относительной частоте  служит доверительный интервал (с приближенными концами
служит доверительный интервал (с приближенными концами  и
и  )
) ,
, (21)
(21)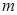 – число появлений события;
– число появлений события;  ;
;  ,
,  . (22)
. (22) , выборочная средняя
, выборочная средняя  и объем выборки
и объем выборки 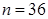 .
. . (23)
. (23) . По таблице приложения 1 находим
. По таблице приложения 1 находим  . Подставив
. Подставив  .
. , если известно среднее квадратическое отклонение
, если известно среднее квадратическое отклонение  нормально распределенной генеральной совокупности.
нормально распределенной генеральной совокупности.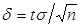 .
. . (24)
. (24)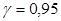 ; следовательно,
; следовательно,  . По таблице приложения 2 найдем
. По таблице приложения 2 найдем  . Подставив
. Подставив  .
. :
: . (25)
. (25) по таблице приложения 4 найдем
по таблице приложения 4 найдем  . Подставив
. Подставив  ,
,  .
.


