Эмпирическая функция распределения
Эмпирической функцией распределения (функцией распределения выборки) называют функцию где
Свойства эмпирической функции: Свойство 1. Значения эмпирической функции принадлежат отрезку Свойство 2. Свойство 3. Если
Пример. Найти эмпирическую функцию по данному распределению выборки:
Решение. Найдем объем выборки Наименьшая варианта Значение следовательно,
Значение
Так как Искомая эмпирическая функция:
График этой эмпирической функции:
Рис. 1. График эмпирической функции
|
, определяющую для каждого значения 
относительную частоту события 
: 
, (1)
– число вариант, меньших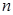 
– объем выборки.
.
– наименьшая варианта, а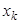 
– наибольшая, то
и 
.
.
.
, поэтому 
.
, а именно 
наблюдалось 5 раз,
.
, а именно: 
наблюдалось 5+15=20 раз:
.
– наибольшая варианта, то 
.
.
