Система дискретных случайных величин
Известно, что если события В этом случае
Рассмотрим дискретную двумерную случайную величину Допустим, что в результате испытания величина В общем случае условные вероятности составляющей будем обозначать так: Условным распределением составляющей Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (1), вычислить условные законы распределения составляющих. Например, условный закон распределения
В общем случае условные законы распределения составляющей Аналогично находят условные законы распределения составляющей
Пример. Дискретная двумерная случайная величина задана табл. 16. Таблица 4
Найти условный закон распределения составляющей Решение. Искомый закон определяется совокупностью следующих условных вероятностей: Заметим, что
Для контроля сложим полученные условные вероятности:
|

 и
и  зависимы, то условная вероятность события
зависимы, то условная вероятность события  отличается от его безусловной вероятности.
отличается от его безусловной вероятности. . (1)
. (1) . Пусть возможные значения составляющих таковы:
. Пусть возможные значения составляющих таковы:  .
. приняла значение
приняла значение  ; при этом
; при этом  примет одно из своих возможных значений:
примет одно из своих возможных значений:  , или
, или  , …, или
, …, или  . Обозначим условную вероятность того, что
. Обозначим условную вероятность того, что  при условии, что
при условии, что  , через
, через  .
.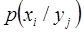
 .
. , называют совокупность условных вероятностей
, называют совокупность условных вероятностей  , вычисленных в предположении, что событие
, вычисленных в предположении, что событие 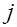 имеет одно и то же значение при всех значениях
имеет одно и то же значение при всех значениях 
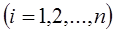 .
. . (2)
. (2) :
: . (3)
. (3)
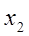

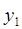

 .
.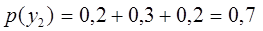 , тогда
, тогда ,
, 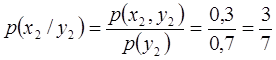 ,
, .
. .
.


