Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)
Двумерная случайная величина задавалась с помощью функции распределения. Непрерывную двумерную величину можно также задать, пользуясь плотностью распределения. Здесь и далее будем предполагать, что функция распределения Плотностью совместного распределения вероятностей
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения. Пример. Найти плотность совместного распределения
Решение. По определению плотности совместного распределения,
Найдем частную производную по
Найдем от полученного результата частную производную по
Искомая плотность совместного распределения равна
Рис. 5. Графическое представление вероятности попадания случайной точки в прямоугольник
Двумерная плотность вероятности имеет следующий вероятностный смысл: вероятность попадания случайной точки
Рис.6. Графическое представление двумерной плотности вероятности
Заметим, что для того, чтобы вычислить вероятность попадания случайной точки Двумерная плотность вероятности обладает следующими свойствами: Свойство 1. Двумерная плотность вероятности неотрицательна: Свойство 2. Двойной несобственный интеграл с бесконечными пределами от двумерной плотности равен 1:
|

 всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка.
всюду непрерывна и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную частную производную второго порядка. двумерной непрерывной случайной величины
двумерной непрерывной случайной величины 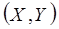 называют вторую смешанную частную производную от функции распределения:
называют вторую смешанную частную производную от функции распределения: .
. системы случайных величин
системы случайных величин  по известной функции распределения
по известной функции распределения .
. .
. от функции распределения:
от функции распределения:
 :
: .
. .
.
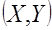 в прямоугольник ABCD (рис. 5) равна
в прямоугольник ABCD (рис. 5) равна

 (рис. 17), достаточно найти двойной интеграл по области
(рис. 17), достаточно найти двойной интеграл по области  .
.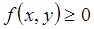 .
. .
.


