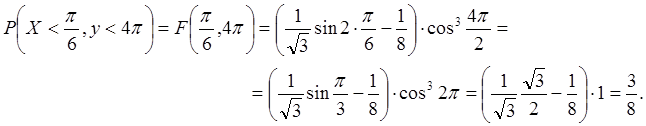Рассмотрим двумерную случайную величину 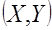 (безразлично, дискретную или непрерывную). Пусть
(безразлично, дискретную или непрерывную). Пусть  – пара действительных чисел. Вероятность события, состоящего в том, что
– пара действительных чисел. Вероятность события, состоящего в том, что 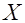 примет значение, меньшее
примет значение, меньшее  , и при этом
, и при этом  примет значение, меньшее
примет значение, меньшее  , обозначим через
, обозначим через  . Если
. Если  и
и  будут изменяться, то будет изменяться и
будут изменяться, то будет изменяться и  , то есть
, то есть  есть функция от
есть функция от  и
и  .
.
Функцией распределения двумерной случайной величины 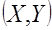 называют функцию
называют функцию  , определяющую для каждой пары чисел
, определяющую для каждой пары чисел  ,
,  вероятность того, что
вероятность того, что 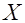 примет значение, меньшее
примет значение, меньшее  , и при этом,
, и при этом,  примет значение, меньшее
примет значение, меньшее 
 .
.
Геометрически это равенство можно истолковать так:  есть вероятность того, что случайная точка
есть вероятность того, что случайная точка 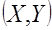 попадет в бесконечный квадрант с вершиной
попадет в бесконечный квадрант с вершиной 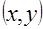 , расположенный левее и ниже этой вершины (рис. 2).
, расположенный левее и ниже этой вершины (рис. 2).
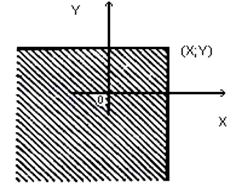
Рис. 2. Геометрическая интерпретация функции распределениядвумерной случайной величины 
Функция распределения  обладает следующими свойствами.
обладает следующими свойствами.
Свойство 1. Значения функции распределения удовлетворяют двойному неравенству  .
.
Свойство 2.  есть неубывающая функция по каждому аргументу, то есть
есть неубывающая функция по каждому аргументу, то есть
 , если
, если  ;
;
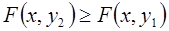 , если
, если  .
.
Свойство 3. Имеют место предельные соотношения:
1)  , 2)
, 2) 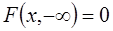 ,
,
3)  , 4)
, 4)  .
.
Свойство 4:
а) При 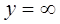 функция распределения системы становится функцией распределения, составляющей
функция распределения системы становится функцией распределения, составляющей 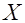 :
:  .
.
б) При  функция распределения системы становится функцией распределения составляющей
функция распределения системы становится функцией распределения составляющей  :
:  .
.
Пример. Найти вероятность того, что в результате испытания составляющая 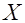 двумерной случайной величины
двумерной случайной величины 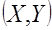 примет значение
примет значение  и при этом составляющая
и при этом составляющая  примет значение
примет значение  , если известна функция распределения системы:
, если известна функция распределения системы:
 .
.
Решение. По определению функции распределения двумерной случайной величины  .
.
Пусть  ,
,  , получим искомую вероятность:
, получим искомую вероятность:
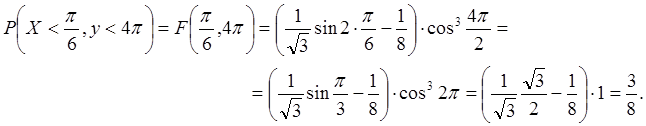

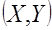 (безразлично, дискретную или непрерывную). Пусть
(безразлично, дискретную или непрерывную). Пусть  – пара действительных чисел. Вероятность события, состоящего в том, что
– пара действительных чисел. Вероятность события, состоящего в том, что 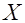 примет значение, меньшее
примет значение, меньшее  , и при этом
, и при этом  примет значение, меньшее
примет значение, меньшее  , обозначим через
, обозначим через  . Если
. Если  .
.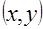 , расположенный левее и ниже этой вершины (рис. 2).
, расположенный левее и ниже этой вершины (рис. 2).
 .
. , если
, если  ;
;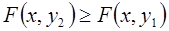 , если
, если  .
. , 2)
, 2) 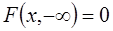 ,
, , 4)
, 4)  .
.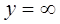 функция распределения системы становится функцией распределения, составляющей
функция распределения системы становится функцией распределения, составляющей  .
. функция распределения системы становится функцией распределения составляющей
функция распределения системы становится функцией распределения составляющей  .
. и при этом составляющая
и при этом составляющая  , если известна функция распределения системы:
, если известна функция распределения системы: .
. .
. ,
,  , получим искомую вероятность:
, получим искомую вероятность: