1. Нормированное распределение Эрланга порядка  описывает распределение среднего арифметического:
описывает распределение среднего арифметического: 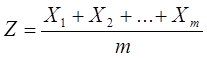 ,
,
где  независимых случайных величин, каждая из которых подчиняется показательному закону с одним и тем же параметром
независимых случайных величин, каждая из которых подчиняется показательному закону с одним и тем же параметром  .
.
2. Случайная величина  , имеющая нормированное распределение Эрланга порядка
, имеющая нормированное распределение Эрланга порядка  , связана со случайной величиной
, связана со случайной величиной 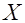 , распределенной по закону Эрланга
, распределенной по закону Эрланга  -го порядка соотношением
-го порядка соотношением  .
.
3. Нормированное распределение Эрланга порядка  описывает распределение суммы
описывает распределение суммы  независимых случайных величин
независимых случайных величин  , каждая из которых распределена по показательному закону с одним и тем же параметром
, каждая из которых распределена по показательному закону с одним и тем же параметром  .
.
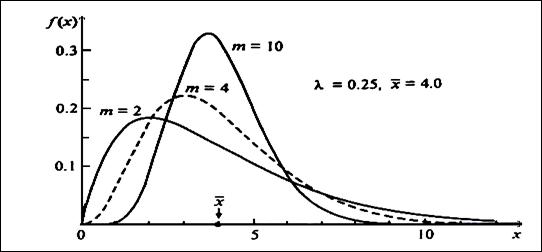
Рис.7. Плотность вероятности нормированного распределения Эрланга
4. Сумма независимых случайных величин, имеющих нормированное распределение Эрланга порядка  с одним и тем же параметром масштаба
с одним и тем же параметром масштаба  имеет нормированное распределение Эрланга порядка
имеет нормированное распределение Эрланга порядка  с тем же самым параметром масштаба
с тем же самым параметром масштаба  .
.
5. При  нормированное распределение Эрланга совпадает с показательным распределением.
нормированное распределение Эрланга совпадает с показательным распределением.
Примечание. При увеличении порядка  математическое ожидание
математическое ожидание  этого распределения остается неизменным, а его дисперсия
этого распределения остается неизменным, а его дисперсия  стремится к нулю. Следовательно, случайная величина
стремится к нулю. Следовательно, случайная величина  , имеющая нормированное распределение Эрланга, «становится все менее и менее случайной» и, в конце концов, вырождается в постоянную
, имеющая нормированное распределение Эрланга, «становится все менее и менее случайной» и, в конце концов, вырождается в постоянную  . Это свойство нормированного распределения Эрланга очень удобно в практических приложениях. Оно позволяет, задаваясь различными значениями
. Это свойство нормированного распределения Эрланга очень удобно в практических приложениях. Оно позволяет, задаваясь различными значениями  , получать различную «степень случайности» случайной величины
, получать различную «степень случайности» случайной величины  – от «сильной случайности», при
– от «сильной случайности», при  до полного отсутствия случайности, при
до полного отсутствия случайности, при 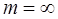 . При этом порядок
. При этом порядок  нормированного распределения Эрланга можно рассматривать как своеобразную «меру случайности» случайной величины
нормированного распределения Эрланга можно рассматривать как своеобразную «меру случайности» случайной величины  , используемой в качестве вероятностной модели какого-либо случайного параметра исследуемого объекта (например, времени прохождения сообщения через систему связи, времени безотказной работы технического устройства и т.п.).
, используемой в качестве вероятностной модели какого-либо случайного параметра исследуемого объекта (например, времени прохождения сообщения через систему связи, времени безотказной работы технического устройства и т.п.).

 описывает распределение среднего арифметического:
описывает распределение среднего арифметического: 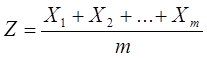 ,
, .
. , имеющая нормированное распределение Эрланга порядка
, имеющая нормированное распределение Эрланга порядка 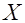 , распределенной по закону Эрланга
, распределенной по закону Эрланга  .
. независимых случайных величин
независимых случайных величин  , каждая из которых распределена по показательному закону с одним и тем же параметром
, каждая из которых распределена по показательному закону с одним и тем же параметром  .
.
 с одним и тем же параметром масштаба
с одним и тем же параметром масштаба  с тем же самым параметром масштаба
с тем же самым параметром масштаба  нормированное распределение Эрланга совпадает с показательным распределением.
нормированное распределение Эрланга совпадает с показательным распределением. этого распределения остается неизменным, а его дисперсия
этого распределения остается неизменным, а его дисперсия  стремится к нулю. Следовательно, случайная величина
стремится к нулю. Следовательно, случайная величина  . Это свойство нормированного распределения Эрланга очень удобно в практических приложениях. Оно позволяет, задаваясь различными значениями
. Это свойство нормированного распределения Эрланга очень удобно в практических приложениях. Оно позволяет, задаваясь различными значениями  до полного отсутствия случайности, при
до полного отсутствия случайности, при 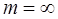 . При этом порядок
. При этом порядок 


