1. Если  – независимые стандартные нормальные случайные величины, то случайная величина
– независимые стандартные нормальные случайные величины, то случайная величина  имеет
имеет  -распределение с
-распределение с 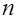 степенями свободы.
степенями свободы.
2.  -распределение с
-распределение с 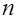 степенями свободы совпадает с гамма-распределением с параметром масштаба
степенями свободы совпадает с гамма-распределением с параметром масштаба  и параметром формы
и параметром формы 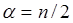 .
.
3. Случайная величина  , имеющая
, имеющая  - распределение с
- распределение с 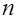 степенями свободы, и случайная величина
степенями свободы, и случайная величина 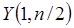 , имеющая гамма-распределение с параметром масштаба
, имеющая гамма-распределение с параметром масштаба  и параметром формы
и параметром формы  , связаны соотношением
, связаны соотношением  ~
~  .
.
4. Сумма независимых случайных величин  , имеющих
, имеющих  -распределение с
-распределение с  степенями свободы соответственно имеет
степенями свободы соответственно имеет  -распределение с
-распределение с 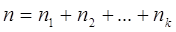 степенями свободы.
степенями свободы.
5. Независимые случайные величины  и
и  , имеющие
, имеющие  -распределение с
-распределение с 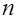 и
и  степенями свободы, соответственно связаны со случайной величиной
степенями свободы, соответственно связаны со случайной величиной  , имеющей
, имеющей  -распределение Фишера-Снедекора с
-распределение Фишера-Снедекора с 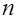 и
и  степенями свободы, соотношением
степенями свободы, соотношением  ~
~  .
.
6. Случайная величина  имеет такое же распределение, как и случайная величина
имеет такое же распределение, как и случайная величина  , то есть
, то есть  ~
~  .
.
7. Случайная величина  , имеющая
, имеющая  -распределение с
-распределение с 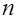 степенями свободы, связана со случайной величиной
степенями свободы, связана со случайной величиной  , имеющей распределение Стьюдента с
, имеющей распределение Стьюдента с 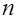 степенями свободы, и независимой от
степенями свободы, и независимой от  стандартной нормальной случайной величиной
стандартной нормальной случайной величиной 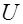 следующим соотношением
следующим соотношением  ~
~  .
.
8. При четном 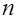 случайная величина
случайная величина  связана со случайной величиной
связана со случайной величиной  , распределенной по закону Пуассона с параметром
, распределенной по закону Пуассона с параметром  , соотношением
, соотношением  .
.
Этому соотношению эквивалентны соотношения
 ,
,  , целое;
, целое;
 ,
,  .
.
Здесь  – интеграл вероятностей
– интеграл вероятностей  -распределения;
-распределения;  – функция распределения Пуассона с параметром
– функция распределения Пуассона с параметром  ;
;  .
.
9. При  случайная величина
случайная величина  сходится к стандартному нормальному распределению. Однако эта сходимость довольно медленная. Гораздо быстрее сходится к стандартному нормальному распределению случайная величина
сходится к стандартному нормальному распределению. Однако эта сходимость довольно медленная. Гораздо быстрее сходится к стандартному нормальному распределению случайная величина  .
.
Распределение  нашло широкое применение при проверке статистических гипотез о виде распределения случайной величины
нашло широкое применение при проверке статистических гипотез о виде распределения случайной величины  , а также в теории надежности – при определении доверительных границ [9].
, а также в теории надежности – при определении доверительных границ [9].
Распределение хи-квадрат может быть определено как сумма квадратов  -независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рис. 7 показаны формы кривых распределения.
-независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рис. 7 показаны формы кривых распределения.
Значения квантилей  -распределения представлены в приложении 3, заимствованные из.
-распределения представлены в приложении 3, заимствованные из.
Пример. При испытаниях системы электроавтоматики распределение отказов по интервалам наработки представлены в табл. 8. Определить по критерию согласия  принадлежность совокупности данного распределения отказов экспоненциальному закону с параметром
принадлежность совокупности данного распределения отказов экспоненциальному закону с параметром  и достоверностью
и достоверностью  .
.
Таблица 3
| Интервал наработок до отказа, ч
| 5-10
| 10-20
| 20-30
| 30-40
| 40-45
| 45-50
|
| Число отказов в интервале
|
|
|
|
|
|
|
Для расчета квантили  -распределения составим дополнительную табл.4.
-распределения составим дополнительную табл.4.
Здесь  – длина интервала.
– длина интервала.
Так как предполагаемый теоретический закон распределения наработки до отказа экспоненциальный, он имеет один параметр. Тогда число степеней свободы равно разности между числом интервалов и числом параметров распределения, то есть  .
.
Таблица 4
Интервал наработок до отказа,  ч ч
| 5-10
| 10-20
| 20-30
| 30-40
| 40-45
| 45-50
| Примечание
|
Число отказов в интервале

|
|
|
|
|
|
|
|
Функция отказов 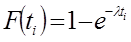 (теоретическая) (теоретическая)
| 0, 98
| 0, 999
| 0, 999
| 0, 999
| 0, 98
| 0, 98
|
|

| 9, 8
| 7, 999
| 5, 994
| 5, 994
| 4, 9
| 4, 9
|
|

| 0, 004
| 0, 000001
| 0, 000006
| 0, 000006
| 0, 002
| 0, 002
| Сумма
0, 008
|
При достоверности  и числе степеней свободы
и числе степеней свободы  по таблице приложения 3 находим квантиль:
по таблице приложения 3 находим квантиль:  .
.
Полученное значение  .
.
Это свидетельствует о том, что гипотеза  о принадлежности статистического распределения теоретическому (экспоненциальному) подтверждается с вероятностью 0, 99.
о принадлежности статистического распределения теоретическому (экспоненциальному) подтверждается с вероятностью 0, 99.
Ответ: статистические данные подтверждают экспоненциальный закон распределения наработки до отказа.

 – независимые стандартные нормальные случайные величины, то случайная величина
– независимые стандартные нормальные случайные величины, то случайная величина  имеет
имеет  -распределение с
-распределение с 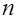 степенями свободы.
степенями свободы. и параметром формы
и параметром формы 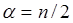 .
. , имеющая
, имеющая 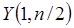 , имеющая гамма-распределение с параметром масштаба
, имеющая гамма-распределение с параметром масштаба  и параметром формы
и параметром формы  , связаны соотношением
, связаны соотношением  ~
~  .
. , имеющих
, имеющих  степенями свободы соответственно имеет
степенями свободы соответственно имеет 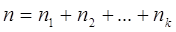 степенями свободы.
степенями свободы. и
и  , имеющие
, имеющие  степенями свободы, соответственно связаны со случайной величиной
степенями свободы, соответственно связаны со случайной величиной  , имеющей
, имеющей  -распределение Фишера-Снедекора с
-распределение Фишера-Снедекора с  ~
~  .
. , то есть
, то есть  .
. , имеющей распределение Стьюдента с
, имеющей распределение Стьюдента с 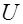 следующим соотношением
следующим соотношением  ~
~  .
. , распределенной по закону Пуассона с параметром
, распределенной по закону Пуассона с параметром  , соотношением
, соотношением  .
. ,
,  , целое;
, целое; ,
,  .
. – интеграл вероятностей
– интеграл вероятностей  – функция распределения Пуассона с параметром
– функция распределения Пуассона с параметром  ;
;  .
. случайная величина
случайная величина  сходится к стандартному нормальному распределению. Однако эта сходимость довольно медленная. Гораздо быстрее сходится к стандартному нормальному распределению случайная величина
сходится к стандартному нормальному распределению. Однако эта сходимость довольно медленная. Гораздо быстрее сходится к стандартному нормальному распределению случайная величина  .
. , а также в теории надежности – при определении доверительных границ [9].
, а также в теории надежности – при определении доверительных границ [9]. -независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рис. 7 показаны формы кривых распределения.
-независимых случайных величин с нулевым средним значением и единичным средним квадратическим отклонением. На рис. 7 показаны формы кривых распределения. и достоверностью
и достоверностью  .
. – длина интервала.
– длина интервала. .
. ч
ч

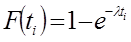 (теоретическая)
(теоретическая)


 и числе степеней свободы
и числе степеней свободы  по таблице приложения 3 находим квантиль:
по таблице приложения 3 находим квантиль:  .
. .
. о принадлежности статистического распределения теоретическому (экспоненциальному) подтверждается с вероятностью 0, 99.
о принадлежности статистического распределения теоретическому (экспоненциальному) подтверждается с вероятностью 0, 99.


