Нормальным называют распределение вероятностей непрерывной случайной величины, которая описывается плотностью
 .
.
Нормальное распределение определяется двумя параметрами:  и
и  . Вероятностный смысл этих параметров:
. Вероятностный смысл этих параметров:
 – есть математическое ожидание,
– есть математическое ожидание,
 – среднее квадратическое отклонение нормального распределения.
– среднее квадратическое отклонение нормального распределения.
Если  и
и  , то нормальное распределение называют нормированным.
, то нормальное распределение называют нормированным.
Плотность нормированного распределения равна  .
.
Эта функция табулирована.
Функция распределения  общего нормального распределения равна:
общего нормального распределения равна:  ,
,
а функция нормированного распределения равна  .
.
Функция  табулирована.
табулирована.
Заметим, что  .
.
Причем  называют квантилью нормированного нормального распределения. Заметим, что нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий.
называют квантилью нормированного нормального распределения. Заметим, что нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий.
График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Он представлен на рис. 2 (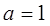 ,
,  ).
).

Рис. 2. График нормальной кривой
Заметим, что параметр « » не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси
» не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси  : вправо, если «
: вправо, если « » возрастает, и влево, если «
» возрастает, и влево, если « » убывает.
» убывает.
С возрастанием параметра  максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси
максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси  ; при убывании
; при убывании  нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси
нормальная кривая становится более «островершинной» и растягивается в положительном направлении оси  .
.
Пусть случайная величина  распределена по нормальному закону. Тогда вероятность того, что
распределена по нормальному закону. Тогда вероятность того, что  примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу  , вычисляется, используя функцию Лапласа
, вычисляется, используя функцию Лапласа  ,
,
которая затабулирована.
Тогда  . (1)
. (1)
Пример. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины  соответственно равны 12 и 3. Найти вероятность того, что в результате испытания
соответственно равны 12 и 3. Найти вероятность того, что в результате испытания  примет значение, заключенное в интервале (14, 16).
примет значение, заключенное в интервале (14, 16).
Решение. Воспользуемся формулой:
 .
.
В данном случае  , тогда
, тогда
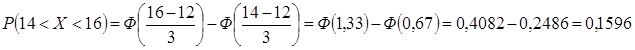 .
.
Пример. Пусть случайная величина, представляющая собой предел текучести стали, замерена в некоторой партии. Известно, что предел текучести подчиняется нормальному распределению со средним значением  МПа и средним квадратическим отклонением
МПа и средним квадратическим отклонением 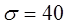 МПа.
МПа.
Найти вероятность того, что значение предела текучести заключено в интервале  МПа и
МПа и  МПа.
МПа.
Решение. Воспользуемся формулой (20), получим


Ответ:  .
.
§ 1.3. Распределение «хи-квадрат»
Пусть  – нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице.
– нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице.
Тогда сумма квадратов этих величин  распределена по закону
распределена по закону  («хи-квадрат») с
(«хи-квадрат») с  степенями свободы; если же эти величины связаны одним линейным соотношением, например
степенями свободы; если же эти величины связаны одним линейным соотношением, например  , то число степеней свободы
, то число степеней свободы 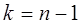 .
.
Плотность этого распределения
 ,
,
где  – гамма-функция; в частности,
– гамма-функция; в частности,  .
.
Отсюда видно, что распределение «хи-квадрат» определяется одним параметром – числом степеней свободы  .
.
С увеличением числа степеней свободы распределение медленно приближается к нормальному.
Заметим, что у случайной величины, имеющей распределение «хи-квадрат», математическое ожидание равно  , а дисперсия
, а дисперсия  , то есть она имеет следующие числовые характеристики (табл. 2).
, то есть она имеет следующие числовые характеристики (табл. 2).
Таблица 2
| Математическое ожидание
| 
|
| Дисперсия
| 
|
| Коэффициент вариации
| 
|
| Асимметрия
| 
|
| Эксцесс
| 
|
| Начальные моменты
|  , ,  , ,
 , ,
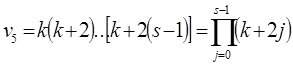
|
| Центральные моменты
|  , , 
|
На рис. 3 представлены графики [1] плотности вероятности 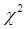 распределения.
распределения.


Рис. 3. Плотность вероятности 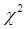 -распределения
-распределения
Заметим, что точками перегиба функции плотности 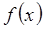 являются точки
являются точки  (при условии, что
(при условии, что  – действительное положительное число).
– действительное положительное число).
Следует отметить, что при  кривая несимметрична, а при
кривая несимметрична, а при  уже приближается к симметричной. При
уже приближается к симметричной. При  кривая
кривая 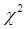 приближается к кривой нормального распределения.
приближается к кривой нормального распределения.

 .
. и
и  . Вероятностный смысл этих параметров:
. Вероятностный смысл этих параметров: и
и  , то нормальное распределение называют нормированным.
, то нормальное распределение называют нормированным. .
. общего нормального распределения равна:
общего нормального распределения равна:  ,
, .
. табулирована.
табулирована. .
. называют квантилью нормированного нормального распределения. Заметим, что нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий.
называют квантилью нормированного нормального распределения. Заметим, что нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий.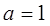 ,
,  ).
).
 : вправо, если «
: вправо, если « .
. распределена по нормальному закону. Тогда вероятность того, что
распределена по нормальному закону. Тогда вероятность того, что  , вычисляется, используя функцию Лапласа
, вычисляется, используя функцию Лапласа  ,
, . (1)
. (1) .
. , тогда
, тогда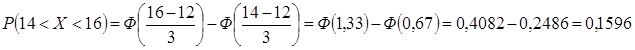 .
. МПа и средним квадратическим отклонением
МПа и средним квадратическим отклонением 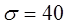 МПа.
МПа. МПа и
МПа и  МПа.
МПа.

 .
. – нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице.
– нормальные независимые случайные величины, причем математическое ожидание каждой из них равно нулю, а среднее квадратическое отклонение – единице. распределена по закону
распределена по закону  («хи-квадрат») с
(«хи-квадрат») с  степенями свободы; если же эти величины связаны одним линейным соотношением, например
степенями свободы; если же эти величины связаны одним линейным соотношением, например  , то число степеней свободы
, то число степеней свободы 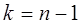 .
. ,
, – гамма-функция; в частности,
– гамма-функция; в частности,  .
. .
. , а дисперсия
, а дисперсия  , то есть она имеет следующие числовые характеристики (табл. 2).
, то есть она имеет следующие числовые характеристики (табл. 2).




 ,
,  ,
,
 ,
,
 ,
, 
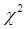 распределения.
распределения.

 являются точки
являются точки  (при условии, что
(при условии, что  – действительное положительное число).
– действительное положительное число). кривая несимметрична, а при
кривая несимметрична, а при  уже приближается к симметричной. При
уже приближается к симметричной. При  кривая
кривая 


