Показательное распределениеПоказательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
где Функция распределения показательного закона
График функции распределения представлен на рис. 10, б. Вероятность попадания в интервал
Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения равны между собой. Заметим, что вероятность того, что непрерывная случайная величина равна
Рис. 5. а) график плотности показательного закона; б) график функции распределения показательного закона
Заметим, что если изучается показательно распределенная случайная величина, причем параметр
|
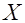, которое описывается плотностью
, (3)
– постоянная положительная величина. График плотности показательного распределения представлен на рис. 5, а.
. (4)
непрерывной случайной величины 
, распределенной по показательному закону
.
.
, где 
– выборочная средняя.
