1. Квантиль  порядка
порядка  F -распределения с
F -распределения с  степенями свободы и квантиль
степенями свободы и квантиль  порядка
порядка  F -распределения с
F -распределения с  степенями свободы связаны соотношением
степенями свободы связаны соотношением  . Этому соотношению
. Этому соотношению
эквивалентно соотношение
 .
.
Приведенные соотношения делают ненужным табулирование F -распределения для значений аргумента  . При необходимости найти значение функции распределения для
. При необходимости найти значение функции распределения для  следует перейти к значению аргумента, равному
следует перейти к значению аргумента, равному  , и воспользоваться последним из приведенных выше соотношений.
, и воспользоваться последним из приведенных выше соотношений.
2. Если  и
и  – независимые случайные величины, имеющие
– независимые случайные величины, имеющие  -распределение с
-распределение с  и
и  степенями свободы соответственно, то случайная величина
степенями свободы соответственно, то случайная величина  имеет F -распределение с
имеет F -распределение с  ,
,  степенями свободы.
степенями свободы.
3. Если случайная величина  имеет F -распределение с параметрами
имеет F -распределение с параметрами  ,
,  , а случайная величина
, а случайная величина  имеет
имеет  -распределение с
-распределение с 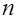 степенями свободы, то справедливы следующие соотношения:
степенями свободы, то справедливы следующие соотношения:
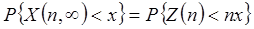 ,
,  ,
,  ~
~  .
.
4. Случайная величина 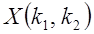 , имеющая F -распределение с
, имеющая F -распределение с  и
и  степенями свободы, связана со случайной величиной
степенями свободы, связана со случайной величиной  , имеющая бета-распределение первого рода с параметрами
, имеющая бета-распределение первого рода с параметрами  ,
,  ,
,
соотношениями

 .
.
Первое из этих соотношений используется для вычисления значений функции распределения  Фишера-Снедекора с помощью таблиц неполной бета-функции.
Фишера-Снедекора с помощью таблиц неполной бета-функции.
Если  – четное число, то F -распределение с параметрами
– четное число, то F -распределение с параметрами  связано с биноминальным распределением с числом испытаний
связано с биноминальным распределением с числом испытаний  и вероятностью успеха
и вероятностью успеха  соотношением
соотношением
 ,
,
где  – случайная величина, распределенная по биноминальному закону с параметрами
– случайная величина, распределенная по биноминальному закону с параметрами 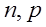 .
.
5. F -распределение сводится к бета-распределению второго рода (распределение VI – по классификации Пирсона).
6. При возрастании  и
и  F -распределение приближается к нормальному распределению.
F -распределение приближается к нормальному распределению.
7. Если  – выборка объема
– выборка объема  из нормальной генеральной совокупности с параметрами
из нормальной генеральной совокупности с параметрами  , а
, а  – выборка объема
– выборка объема 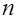 совокупности с параметрами
совокупности с параметрами  ,
,
то статистика:  .
.
имеет F -распределение Фишера-Снедекора с  и
и  степенями свободы. (Здесь
степенями свободы. (Здесь  и
и  – выборочные оценки математических ожиданий
– выборочные оценки математических ожиданий  и
и  соответственно).
соответственно).

 порядка
порядка  F -распределения с
F -распределения с  степенями свободы и квантиль
степенями свободы и квантиль  порядка
порядка  F -распределения с
F -распределения с  степенями свободы связаны соотношением
степенями свободы связаны соотношением  . Этому соотношению
. Этому соотношению .
. . При необходимости найти значение функции распределения для
. При необходимости найти значение функции распределения для  , и воспользоваться последним из приведенных выше соотношений.
, и воспользоваться последним из приведенных выше соотношений. и
и  – независимые случайные величины, имеющие
– независимые случайные величины, имеющие  -распределение с
-распределение с  и
и  степенями свободы соответственно, то случайная величина
степенями свободы соответственно, то случайная величина  имеет F -распределение с
имеет F -распределение с  имеет F -распределение с параметрами
имеет F -распределение с параметрами  ,
,  , а случайная величина
, а случайная величина  имеет
имеет 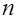 степенями свободы, то справедливы следующие соотношения:
степенями свободы, то справедливы следующие соотношения: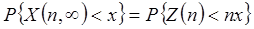 ,
,  ,
,  ~
~  .
.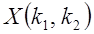 , имеющая F -распределение с
, имеющая F -распределение с  , имеющая бета-распределение первого рода с параметрами
, имеющая бета-распределение первого рода с параметрами  ,
,  ,
,
 .
. Фишера-Снедекора с помощью таблиц неполной бета-функции.
Фишера-Снедекора с помощью таблиц неполной бета-функции. – четное число, то F -распределение с параметрами
– четное число, то F -распределение с параметрами  связано с биноминальным распределением с числом испытаний
связано с биноминальным распределением с числом испытаний  и вероятностью успеха
и вероятностью успеха  соотношением
соотношением ,
, – случайная величина, распределенная по биноминальному закону с параметрами
– случайная величина, распределенная по биноминальному закону с параметрами 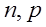 .
. – выборка объема
– выборка объема  из нормальной генеральной совокупности с параметрами
из нормальной генеральной совокупности с параметрами  , а
, а  – выборка объема
– выборка объема  ,
, .
. и
и  степенями свободы. (Здесь
степенями свободы. (Здесь  и
и  – выборочные оценки математических ожиданий
– выборочные оценки математических ожиданий  и
и  соответственно).
соответственно).


