Комплексный спектр единичного импульса
S( j w ) = и совпадает со своим модулем: | S( j w ) | = S( w ) = 1. Спектр амплитуд - сплошной, простирающийся до бесконечно больших значений w с неизменной спектральной плотностью при всех частотах, равной 1. Если бесконечный спектр d-сигнала ограничить частотой среза wс (как показано на рис.), то единичный импульс принимает вид сигнала, описываемого функцией вида sin w сt/ w сt. Её называют во многих литературных источниках функцией отсчётов и обозначают Sa( a ). Такая функция равна 1 при a=0 (при нулевом аргументе), а с увеличением a изменяется по закону затухающего синуса/
Одиночный прямоугольный импульс в соответствии с прямым преобразованием Фурье имеет спектр
|

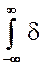 (t) e-j w tdt =
(t) e-j w tdt = 
 (t)e-j w tdt = e-j w 0
(t)e-j w tdt = e-j w 0 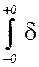 (t) dt = 1,
(t) dt = 1, Сигналы d (t), как и 1(t), являются идеализацией реальных сигналов и также используются как элементарные сигналы для описания более сложных
Сигналы d (t), как и 1(t), являются идеализацией реальных сигналов и также используются как элементарные сигналы для описания более сложных
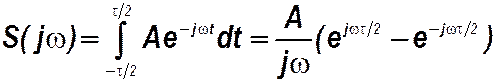 =
=  .
.


