Финансовые ренты (аннуитеты) и их практическое использование
Финансовой рентой или аннуитетом называется ряд последовательных фиксированных платежей, производимых через равные промежутки времени. Финансовые ренты (аннуитеты) характеризуются такими параметрами: 1) член ренты — величина каждого отдельного платежа; 2) период ренты — временной интервал между двумя платежами; 3) срок ренты — время от начала реализации ренты до момента начисления последнего платежа; 4) процентная ставка — ставка, используемая для расчета наращения платежей, составляющих ренту. Кроме того, рента характеризуется: количеством платежей в год, частотой начисления процентов, моментом производства платежа (в начале, середине или в конце года) и т.д. [66, с. 91]. Обобщающими показателями ренты (аннуитета) являются будущая (наращенная) и текущая или настоящая (приведенная) ее величина. Будущая стоимость аннуитета — это сумма всех членов потока платежей с начисленными на них процентами на конец срока, т.е. на дату последней выплаты [66, с. 91]. Для определения будущей стоимости обычного аннуитета можно использовать формулу:
где F — будущая стоимость обычного аннуитета; C — величина ежегодного взноса (платежа); t — срок аннуитета; n — процентная ставка;
В практике финансовых расчетов с использованием аннуитетов могут быть различные варианты рентных платежей и начисления процентов. Рассмотрим 4 возможных вариантов аннуитетов. 1. Рентные платежи вносятся раз в год, а проценты на них начисляются несколько раз в году, например, (m) раз в году. В этом случае будущая стоимость аннуитета определяется по формуле:
2. Рентные платежи вносятся несколько раз в течение года равными суммами, а начисление процентов производится один раз в конце года. При таких условиях будущая стоимость аннуитета может быть определена:
где р — число рентных платежей в течение года. 3. Рентные платежи вносятся (р) раз в году, начисление процентов производится (m) раз в году, число периодов начисления процентов в течение года равно числу рентных платежей в течение года, т.е. m = p. В этом случае будущая стоимость аннуитета определяется по формуле:
где n — номинальная ставка процентов; t — срок ренты в годах; m — число периодов начисления процентов в течение года. 4. Рентные платежи вносятся (р) раз в году, начисление процентов производится (m) раз в году, число рентных платежей не равно числу периодов начисления процентов, т.е. p ¹ m. Будущая стоимость аннуитета может быть определена из формулы:
где р — число рентных платежей в течение года; m — число периодов начисления процентов в течение года; n — номинальная процентная ставка; t — срок ренты. Пример 4.24. Рентные платежи выплачиваются в течение 5 лет в размере 10 тыс. грн. Процентная ставка 12% годовых. Определить будущую стоимость аннуитета при следующих условиях: а) платежи вносятся один раз в год, а проценты начисляются поквартально; б) платежи вносятся 2 раза в год равными суммами, а проценты начисляются один раз в год; в) рентные платежи вносятся поквартально, проценты начисляются поквартально; г) рентные платежи вносятся ежеквартально, а проценты начисляются по полугодиям. Решение: Используем формулы (4.50), (4.51), (4.52), (4.53) а) б) в) г) При осуществлении финансовых вычислений иногда возникает необходимость определения размеров разовых платежей и срока аннуитета. Величина рентного платежа может быть определена по формуле:
Срок аннуитета определяется по формуле:
Настоящая величина потока рентных платежей — это сумма всех его членов, уменьшенная (дисконтированная) на величину процентной ставки на определенный момент времени, совпадающий с началом потока платежей, или предшествующий ему. Настоящая величина показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые бы начислялись установленные проценты в течение срока ренты, можно было обеспечить получение наращенной суммы. Оценка настоящей величины производится на момент начала реализации ренты. Для ренты с членами, равными (С), настоящая величина определяется по формуле:
где А — настоящая величина потока рентных платежей; С — сумма рентного платежа; а — коэффициент приведения ренты, показывающий, сколько рентных платежей (С) содержится в настоящей величине. Коэффициент приведения ренты (а) определяется по формуле:
Пример 4.25. Семья желает в течение 3 лет собрать сумму для приобретения автомобиля стоимостью 95 тыс. гр. Она может выделить на эти цели 28 тыс. гр. ежегодно, помещая их в банк под 12, 5% годовых (проценты сложные). Какая сумма потребовалось бы семье для приобретения автомобиля стоимостью 95 тыс. гр., если бы он ее поместил бы в банк на 3 года под 12, 5% годовых? Решение: С = 28 тыс. гр.; t = 3; n = 12, 5%.
Наращенная сумма при ежегодных платежах в размере 28 тыс. гр. под 12, 5% годовых составит:
Из этого примера можно вывести математическую взаимосвязь величин:
или
При начислении процентов (m) раз в году настоящая величина аннуитета вычисляется по формуле:
При внесении рентных платежей несколько раз в году и начислении процентов 1 раз в году настоящая величина аннуитета может быть определена по формуле:
где р — число рентных платежей. При условии, что число рентных платежей не равняется числу начисления процентов (p ≠ m) используется формула:
При расчете настоящей величины аннуитета достаточно часто возникает необходимость определения срока ренты. Срок ренты при расчете настоящей приведенной величины аннуитета определяется по формуле:
Размер годового платежа может быть определен по формуле:
Вопросы для самоконтроля:
1. В чем состоят объективные причины учета фактора времени в финансовых расчетах? 2. В чем состоят субъективные причины учета фактора времени в финансовых расчетах? 3. Назовите основные факторы, влияющие на изменение стоимости денег во времени. 4. Охарактеризуйте основные факторы, влияющие на стоимость денег во времени. 5. Что такое наращение и дисконтирование? 6. Что такое проценты? 7. Дайте понятие процентной ставки. 8. Назовите виды процентных ставок. 9. Какие способы начисления процентов Вы можете назвать? 10. Какие схемы начисления процентных ставок Вы знаете? 11. Что такое капитализация процентов? 12. Что такое будущая стоимость денег? 13. Как можно определить будущую стоимость денег при простых и сложных процентах? 14. Как можно определить будущую стоимость денег по схеме простых процентов? 15. Как можно определить будущую стоимость денег по схеме сложных процентов? 16. Для каких целей используется оценка будущей стоимости денег? 17. Как определить эффективную годовую процентную ставку? 18. Для каких целей применяется эффективная годовая процентная ставка? 19. Как определяется будущая стоимость денег при внутригодовых начислениях сложных процентов? 20. Как в финансовых расчетах будущей стоимости учитывается инфляция? 21. Как определить простую и сложную процентную ставку с учетом инфляции? 22. Что такое настоящая стоимость денег? 23. Как определяется настоящая стоимость денег по простым и сложным процентным дисконтным ставкам? 24. Что такое дисконтная процентная ставка? 25. Что такое дисконт? 26. Какие методы определения настоящей стоимости денег Вам известны? 27. Как определяется настоящая стоимость денег по простой дисконтной ставке? 28. Как определяется настоящая стоимость денег по сложной дисконтной ставке? 29. Для каких целей применяется оценка денег по настоящей стоимости? 30. Что такое финансовая рента? 31. Характеристика финансовой ренты. 32. Основные виды расчетов финансовой ренты при оценке ее будущей стоимости. 33. Основные виды расчетов финансовой ренты при оценке ее настоящей стоимости. 34. Как определить размер рентного платежа при обыкновенном аннуитете? 35. Срок аннуитета при расчете настоящей стоимости ренты.
раздел 5
|

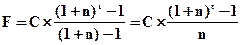 , (4.49)
, (4.49) — коэффициент наращения аннуитета.
— коэффициент наращения аннуитета. . (4.50)
. (4.50)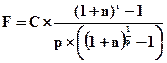 , (4.51)
, (4.51) , (4.52)
, (4.52) , (4.53)
, (4.53) тыс. гр.
тыс. гр. тыс. гр.
тыс. гр. тыс. гр.
тыс. гр.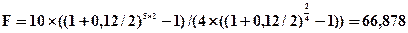 тыс. гр.
тыс. гр. . (4.54)
. (4.54) . (4.55)
. (4.55) , (4.56)
, (4.56)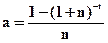 . (4.57)
. (4.57) тыс. гр.
тыс. гр. тыс. гр.
тыс. гр.
 . (4.58)
. (4.58) . (4.59)
. (4.59) . (4.60)
. (4.60)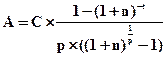 , (4.61)
, (4.61) . (4.62)
. (4.62)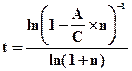 . (4.63)
. (4.63) . (4.64)
. (4.64)


