Вопрос 1. Понятие «простые проценты», формула простого процента, наращение по простым процентам
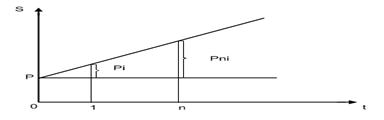
Рассмотрим процесс наращения (accumulation), т.е. определения денежной суммы в будущем, исходя из заданной суммы сейчас. Экономический смысл операции наращения состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Здесь идет движение денежного потока от настоящего к будущему. При использовании простых ставок процентов проценты (процентные деньги) определяются исходя из первоначальной суммы долга. Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов. Под наращенной суммой ссуды понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока. Пусть P - первоначальная сумма денег; i - ставка простых процентов. Начисленные проценты за один период равны P*i, а за n периодов равны P*n*i Процесс изменения суммы долга с начисленными процентами описывается арифметической прогрессией, членами которой являются P, P+P*i = P(1+i); P(1+i)+P*i=P(1+2i); и т.д. до P(1+n*i) S=P(1+ni) - является наращенной суммой к концу n-го промежутка начисления. Формула S=P(1+ni) называется формулой наращения по простым процентам. Множитель (1+ni) является множителем наращения, т.е. показывает во сколько раз наращенная сумма больше первоначальной. Процесс роста суммы долга по простым процентам можно представить графически:
Таким образом, размер ожидаемого дохода зависит от трех факторов: от величины инвестированной суммы, от уровня процентной ставки и от срока финансовой операции. Наращенную сумму можно представить в виде слагаемых: первоначальные суммы Р и суммы процентов I, S=P+I (2), где I=Pni. Следует заметить, что задачи на простые проценты на практике встречаются редко, поскольку к простым процентам прибегают в случаях: 1. выдачи краткосрочных ссуд, т.е. ссуд, срок которых либо равен году, либо меньше его, с однократным начислением процентов; 2. когда проценты не присоединяются к сумме долга, а периодически выплачиваются. В тех случаях, когда срок ссуды менее года, происходит модификация формулы.Поэтому при продолжительности ссуды менее года необходимо выяснить какая часть процентов уплачивается кредитору. Для этого величину n выражают в виде дроби: n – срок ссуды, измеренный в долях года; k – число дней в году, временная плата; t – срок операции, ссуде в днях Расчет числа дней пользования ссудой может быть точным или приближенным комбинируя различные варианты временной базы и методом подсчета в ней ссуды получают 3 варианта расчета процентов, применяемых на практике: 1) германская схема; 2) французская схема; 3) английская схема.
|

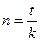 , где
, где


