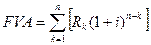Вопрос 1. Потоки с разовыми изменениями платежей
В финансовых операциях возможны ситуации, когда величина платежа либо увеличивается, либо уменьшается с течением времени, например, под влиянием инфляции. Например, при заключении договоров аренды в условиях инфляции может предусматриваться периодическое увеличение платежа, компенсирующее негативное влияние изменения цен. Величина амортизационных отчислений может меняться в связи с изменением количества и стоимости основных фондов. Договор стандартного возрастающего страхования жизни предполагает ежегодный рост страховой суммы на величину страховой суммы первого года страхования. Для гарантии возврата взятого страхователем кредита используется стандартное убывающее страхование жизни. В такого рода случаях поток платежей представляет собой переменный аннуитет (ренту) и для определения будущей или приведенной стоимости аннуитета необходимо знать соответствующие формулы.. однако, когда члены аннуитета изменяются в соответствии с некоторыми законами, эти формулы упрощаются. Предположим, что имеется аннуитет постнумерандо, платежи которого образуют арифметическую прогрессию с первым членом Если Если Сложив наращенные члены аннуитета, сгруппировав отдельные слагаемые и умножив на Аналогичным образом можно получить оценки аннуитета для других ситуаций. Пусть имеется аннуитет постнумерандо, платежи которого образуют геометрическую прогрессию с первым членом Если даже члены переменного аннуитета не образуют арифметическую и геометрическую прогрессии, то все равно во многих случаях оценка аннуитета может все же выполняться путем несложных расчетов с помощью финансовых таблиц. Нерегулярные потоки платежей характеризуются присутствием хотя бы одного нерегулярного параметра: период ренты или размер платежа. Для получения их обобщающих характеристик требуется прямой счет, т.е. вычисление соответствующих характеристик по каждому платежу и последующему их суммированию. Однако в ряде случаев можно применять следующую формулу:
|

 и разностью
и разностью 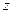 . В этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов. Если число периодов равно
. В этом случае говорят о переменном аннуитете с постоянным абсолютным изменением его членов. Если число периодов равно 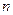 ,
,  является процентной ставкой за базовый период, в соответствии с которой один раз в конце периода начисляются сложные проценты и период аннуитета совпадает с базовым, то наращенный денежный поток имеет вид:
является процентной ставкой за базовый период, в соответствии с которой один раз в конце периода начисляются сложные проценты и период аннуитета совпадает с базовым, то наращенный денежный поток имеет вид:  ,
,  ,
, 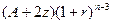 , …….,
, ……., 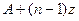 .
.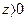 , то члены аннуитета возрастают.
, то члены аннуитета возрастают.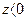 , то члены аннуитета убывают и число этих членов должно удовлетворять неравенству
, то члены аннуитета убывают и число этих членов должно удовлетворять неравенству 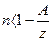 , иначе можно получить отрицательные платежи, что лишено смысла.
, иначе можно получить отрицательные платежи, что лишено смысла.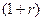 в результате получим:
в результате получим: 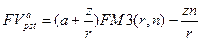 .
.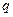 . В этом случае говорят о переменном аннуитете с постоянным относительным изменением его членов. Если
. В этом случае говорят о переменном аннуитете с постоянным относительным изменением его членов. Если 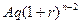 , ….,
, ….,  ,
, 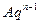 . И
. И 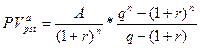 .
.