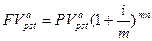Вопрос 2. Наращенная сумма постоянной ренты постнумерандо: годовая рента, начисление процентов m раз в году, непрерывное начисление процентов
При рассмотрении финансовой ренты (аннуитета) используются основные категории: 1. член ренты (R) – величина каждого отдельного платежа; 2. период ренты (t) – временной интервал между членами ренты; 3. срок ренты (n) – время от начала финансовой ренты до конца последнего ее периода; 4. процентная ставка (i) – ставка, используемая при наращении платежей, из которых состоит рента. Рента (аннуитет) называется постоянным, если все денежные потоки (поступления) равны между собой, т.е. С1=С2=…=Сn=А. Поток постнумерандо. Прямая задача оценка аннуитета при заданных величинах регулярного поступления (А) и процентной ставки (i) предполагает оценку будущей стоимости аннуитета. Наращенный денежный поток: А(1+i)n-1; А(1+i)n-2; …; А(1+i); А Будущая стоимость денежного потока может быть рассчитана по формуле:
Значение множителя для различных сочетаний i и n можно табулировать. Иногда множитель Так как оценка срочных аннуитетов необходима при анализе финансовых операций, тогда, если i-процентная ставка за базовый период, а начисление сложных процентов происходит m-раз в течение этого периода, то наращенный поток, начиная с последнего денежного поступления, имеет вид:
Пусть в течение базового периода денежные поступления p - раз, а i-процентная ставка, начисляемая в конце периода, тогда:
Пусть в течение базового периода денежные поступления происходят p – раз и проценты начисляются m-раз за период, тогда:
Обратная задача оценки будущих денежных поступлений с позиции текущего момента, с которого отчитываются временные интервалы, входящие в аннуитет. Оценка текущей стоимости аннуитета постнумерандо имеет вид: Где Множитель Начисление m-раз за базовый период:
Начисление процентов 1 раз за базовый период и m-раз за базовый период:
Зависимость между будущей и приведенной стоимостями аннуитета постнумерандо, начисление процентов n-раз за период:
|

 , где
, где 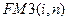 – называется коэффициентом наращения аннуитета.
– называется коэффициентом наращения аннуитета. - показывает, чему будет равна суммарная величина срочного аннуитета в 1 ден. ед. к концу срока его действия.
- показывает, чему будет равна суммарная величина срочного аннуитета в 1 ден. ед. к концу срока его действия. называется коэффициентом аккумуляции вклада или фактора будущей стоимости аннуитета.
называется коэффициентом аккумуляции вклада или фактора будущей стоимости аннуитета. и
и
 - сложные проценты
- сложные проценты - простые проценты
- простые проценты


 - называется коэффициентом дисконтирования ренты (аннуитета). Показывает, чему равен с позиции текущего момента стоимость аннуитета с регулярными денежными поступлениями в размере 1 ден.ед., продолжающейся n-равных периодов, заданной процентной ставкой i.
- называется коэффициентом дисконтирования ренты (аннуитета). Показывает, чему равен с позиции текущего момента стоимость аннуитета с регулярными денежными поступлениями в размере 1 ден.ед., продолжающейся n-равных периодов, заданной процентной ставкой i.