Вопрос 3. Замена ставок на среднюю процентную ставку

Изменение сроков платежей. Объединение нескольких платежей в один (консолидация платежей) с установлением срока его погашения и т.д. В результате любых изменений ни один из участников не должен терпеть убытки. В этих случаях руководствуются принципом финансовой эквивалентности, устанавливающим неизменность финансовых отношений участников до и после изменения финансовых соглашений.

Простые проценты.

Пусть платеж Р₁ со сроком n₁ необходимо заменить платежом Р₀ со сроком n₀, сроки измеряются от одного момента времени и процентная ставка равна i. Тогда уравнение эквивалентности имеет вид:

, если n₀ > n₁

, если n₀ = n₁

 

, если n₀ < n₁

 

 

Уравнение эквивалентности относительно n₀ имеет вид:

 

, если Р₀ > Р₁

 

, если Р₀ = Р₁

 

, если Р₀ < Р₁

 

При замене платежей применяются и учетные ставки:

 

, если n₀ > n₁

, если n₀ = n₁

 

, если n₀ < n₁

 

, если Р₀ > Р₁

 

, если Р₀ = Р₁

 

, если Р₀ < Р₁

Сложные проценты.

Если платеж , со сроком необходимо заменить платежом , со сроком при использовании сложной процентной ставки i, и измеряются от одного момента времени, то уравнение эквивалентности:

При известном платеже новый срок определяется по формуле:

Если платежи , выплачиваемые соответственно через время заменяются одним платежом с выплатой через , то:

И

Если несколько платежей заменяются одним и при этом используется номинальная годовая процентная ставка J, т.е. сложные проценты начисляются m-раз в год, то уравнение эквивалентности:

И

Если платежи , выплачиваемые соответственно через время , консолидируются в один платеж с выплатой через время и используется номинальная годовая учетная ставка d, тогда:

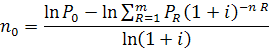
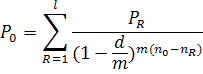И