Сравнение
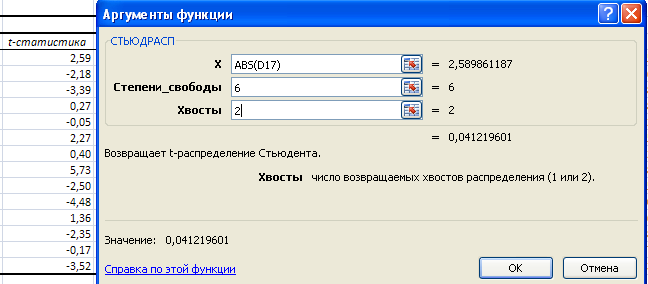
Исходя из таблицы 11, коэффициенты при переменной Район, Общая площадь, Жилая площадь, Площадь кухни, Плита являются значимым на 5%-ном уровне. Это утверждение подтверждается и при расчете р-значения – вероятности для t-распределения Стьюдента. Расчет р-значения возможен с помощью функции СТЬЮДРАСП (Рисунок 7). Синтаксис функции: СТЬЮДРАСП(x; степени_свободы; хвосты) x — числовое значение, для которого требуется вычислить распределение. (модуль t-значения) Степени_свободы — целое, указывающее число степеней свободы (n-p-1). Хвосты — число возвращаемых хвостов распределения. Если хвосты = 1, функция СТЬЮДРАСП возвращает одностороннее распределение. Если хвосты = 2, функция СТЬЮДРАСП возвращает двустороннее распределение (в практической работе распределение двустороннее).
Рисунок 7. Использование функции СТЬЮДРАСП в Excel.
Рассчитаем р-значение для каждого фактора. Если полученное значение меньше 0, 05 коэффициент регрессии является значимым. Нижние 95% и верхние 95% рассчитываются для построения доверительного интервала коэффициента. Следует заметить, что вообще доверительный интервал имеет смысл строить только для значимых коэффициентов регрессии. Для расчета нижних 95% используется формула
Для расчета верхних 95% используется формула
Таблица 12.
|

 (12).
(12). (13).
(13).


