Регрессионная статистика
Заполнение таблицы «Дисперсионный анализ» Большая часть данных уже получена выше. (Объясняемая и необъясняемая ошибка). Рассчитаем t wx: val=" Cambria Math" /> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> 13< /m: t> < /m: r> < /m: den> < /m: f> < m: r> < m: rPr> < m: sty m: val=" p" /> < /m: rPr> < w: rPr> < w: rFonts w: ascii=" Cambria Math" /> < wx: font wx: val=" Cambria Math" /> < w: sz w: val=" 28" /> < w: sz-cs w: val=" 28" /> < /w: rPr> < m: t> = 1342712, 27< /m: t> < /m: r> < /m: oMath> < /m: oMathPara> < /w: p> < w: sectPr wsp: rsidR=" 00000000" > < w: pgSz w: w=" 12240" w: h=" 15840" /> < w: pgMar w: top=" 1134" w: right=" 850" w: bottom=" 1134" w: left=" 1701" w: header=" 720" w: footer=" 720" w: gutter=" 0" /> < w: cols w: space=" 720" /> < /w: sectPr> < /w: body> < /w: wordDocument> "> Оценку статистической значимости уравнения регрессии в целом проведем с помощью F -критерия Фишера. Уравнение множественной регрессии значимо (иначе – гипотеза H0 о равенстве нулю параметров регрессионной модели, т.е.
где Фактическое значение F - критерия по формуле составит:
Для расчета табличного значения критерия Фишера используется функция FРАСПОБР (Рисунок 4). Степень свободы 1: p=13 Степень свободы 2: n-p-1 = 20-13-1=6
Рисунок 4. Использование функции FРАСПОБР в Excel.
Fтабл = 3, 976 < 16, 88, следовательно, модель адекватна опытным данным. Значимость F рассчитывается с помощью функции FРАСП. Эта функция возвращает F-распределение вероятности (распределение Фишера) и позволяет определить, имеют ли два множества данных различные степени разброса результатов.
Рисунок 5. Использование функции FРАСП в Excel. Значимость F = 0, 001. Таблица 10.
|

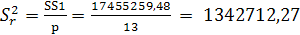 .
.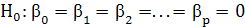 отвергается), если
отвергается), если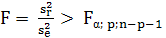 , (10)
, (10)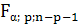 - табличное значение F-критерия Фишера.
- табличное значение F-критерия Фишера.