Пример 1. По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия у (млн руб.) от цен на сырье х1 (тыс
По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия у (млн руб.) от цен на сырье х1 (тыс. руб. на 1 т) и производительности труда х2 (ед. продукции на 1 работника):
При анализе остаточных величин были использованы значения, приведенные в табл. 3.1. Таблица 4.1
Требуется: 1. По трем позициям рассчитать 2. Рассчитать критерий Дарбина - Уотсона. 3. Оценить полученный результат при 5%-ном уровне значимости. 4. Указать, пригодно ли уравнение для прогноза.
Решение 1. yt определяется путем подстановки фактических значений х1 и х2 в уравнение регрессии:
Остатки ε 1 рассчитываются по формуле
ε t = yt -
Следовательно, ε 1 = 210 – 200 = 10, ε 2 = 720 – 700 = 20, ε 3 = 300 – 350 = - 50;
ε t-1 - те же значения, что и ε t, но со сдвигом на один месяц.
Результаты вычислений оформим в виде табл. 3.2.
Таблица 4.2
2. Критерий Дарбина - Уотсона рассчитывается по формуле
3. Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При п = 18 месяцев и от = 2 (число факторов) нижнее значение d’ равно 1, 05, а верхнее - 1, 53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:
4 - d = 4 - 3, 81 = 0, 19,
что значительно меньше, чем d'. Это означает наличие в остатках автокорреляции. 4. Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна, а может быть, в рядах динамики имеется общая тенденция.
|

 = 200 - l, 5 ∙ x1 + 4, 0 ∙ x2.
= 200 - l, 5 ∙ x1 + 4, 0 ∙ x2. = 10500, Σ (ε t – ε t-1)2 = 40 000.
= 10500, Σ (ε t – ε t-1)2 = 40 000.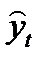 , ε t, ε t-1, ε t 2, (ε t – ε t-1).
, ε t, ε t-1, ε t 2, (ε t – ε t-1). 1= 200 - 1, 5 ∙ 800 + 4, 0 ∙ 300 = 200;
1= 200 - 1, 5 ∙ 800 + 4, 0 ∙ 300 = 200; 2 = 200 - 1, 5 ∙ 1000 + 4, 0 ∙ 500 = 700;
2 = 200 - 1, 5 ∙ 1000 + 4, 0 ∙ 500 = 700; ;
;



