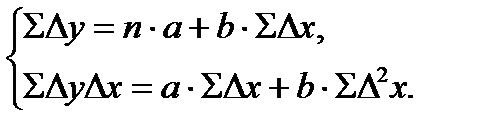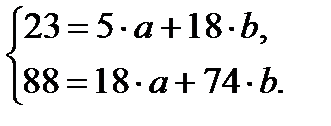Пример 2. Имеются следующие данные о величине дохода на одного члена
Имеются следующие данные о величине дохода на одного члена семьи и расхода на товар A (табл. 3.3).
Таблица 4.3
Требуется: 1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда. 2. Перечислить основные пути устранения тенденции для построения модели спроса на товар А в зависимости от дохода. 3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов. 5. Пояснить экономический смысл коэффициента регрессии. 6. Построить линейную модель спроса на товар А, включив в нее фактор времени. Интерпретировать полученные параметры.
Решение 1. Обозначим расходы на товар А через у, а доходы одного члена семьи - через х. Ежегодные абсолютные приросты определяются по формулам Δ yt = yt – yt-1, Δ xt = xt – xt-1. Расчеты можно оформить в виде таблицы (табл. 3.4). Таблица 4.4
Значения Δ y имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х: абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией. 2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. Δ y = f(Δ x), если ряды динамики характеризуются линейной тенденцией. Другой возможный путь учета тенденции при построении моделей - найти по каждому ряду уравнение тренда:
и отклонения от него: dy = yt -
Далее модель строится по отклонениям от тренда:
dy=f(dx).
При построении эконометрических моделей чаще используется другой путь учета тенденции - включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т.е.
3. Модель имеет вид Δ
Для определения параметров а и b применяется МНК. Система нормальных уравнений следующая:
Применительно к нашим данным имеем
Решая эту систему, получим: а = 2, 565 и b = 0, 565, откуда модель имеет вид Δ
4. Коэффициент регрессии b = 0, 565 руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар А увеличиваются со средним ускорением, равным 0, 565 руб.
5. Модель имеет вид
Применяя МНК, получим систему нормальных уравнений:
Расчеты оформим в виде табл. 3.5. Таблица 4.5
Система уравнений примет вид
Решая ее, получим а = -5, 42; b = 0, 322; с = 3, 516.
Уравнение регрессии имеет вид у = -5, 42 + 0, 322 • х + 3, 516 • t.
Параметр b = 0, 322 фиксирует силу связи y и х. Его величина означает, что с ростом дохода на одного члена семьи на 1 %-ный пункт при условии неизменной тенденции расходы на товар А возрастают в среднем на 0, 322 руб. Параметр с = 3, 516 характеризует среднегодовой абсолютный прирост расходов на товар А под воздействием прочих факторов при условии неизменного дохода.
|

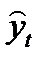 = f(t) и
= f(t) и  = f(t)
= f(t) = а + b ∙ Δ х.
= а + b ∙ Δ х.