Исходные данные транспортной задачи
Решим задачу симплекс-методом. Запишем ограничения модели: 1. Продукция, отправляемая из каждого пункта производства, не должна превышать ее количества, имеющегося в наличии. X1 + X2 + X3 + X4 = 6. X5 + X6 + X7 + X8 = 8. X9 + X10 + X11 + X12 = 10.
2. Продукция, поступающая в каждый пункт потребления, должна удовлетворять потребности в ней. X1 + X5 + X9 = 4. X3 + X7 + X11 = 8. X2 + X6 + X10 = 6. X4 + X8 + X12 = 6. Требуется определить наименьшую сумму транспортных издержек: F(x) = X1 + 2X2 + 3X3 + 4X4 + 4X5 + 3X6 +2X7 + 2X10 + 2X11 + X12 ®min.
Решение транспортной задачи симплекс-методом основано на отыскании базисных переменных. Выразим базисные переменные: X1 = 6 – X2 – X3 – X4. X10 = -2 – X2 + X5 + X7 + X8. (1) X6 = 8 – X5 – X7 - X8. X11 = 8 –X3 –X7. (2) X12 = 6 – X4 – X8. X9 = -2 + X2 + X3 + X4 – X5. (3) Получено 6 уравнений, следовательно, должно быть шесть базисных неизвестных, которые и найдем из каждого уравнения. Базисные переменные X1, X6, X9, X10, X11, X12, а свободные – X2, X3, X4, X5, X7, X8. Выразим через свободные члены целевую функцию: F(x) = 6 – X2 – X3 – X4 + 2X2 + 3X3 + 4X4 + 4X5 + 24 – 3X5 –3X7 - 3X8 + 2X7 – - 4 – 2X2 + 2X5 + 2X8 + 2X7 + 16 – 2X3 - 2X7 + 6 – X4 – X8 = 48 – X2 + 2X4 + + 3X5 – X7 – 2X8. Так как при решении задач на минимум в целевой функции должны быть только положительные элементы, то заменим базисный член X6 на свободный X7. Получим X7 = 8 – X5 – X8 – X6. (4) Запишем новую целевую функцию: F(x) = 48 – X2 + 2X4 + 3X5 - 8 + X5 + X8 + X6 – 2X8 = 40 – X2 + 2X4 + 4X5 - - X8 + X6. Заменим базисный член X12 на свободный X8. Получим X8 = 6 – X4 – X12 (5) Запишем новую целевую функцию: F(x) = 34 – X2 + 3X4 + X12 + 4X5 + X6. Заменим базисный член X1 на свободный X2. Получим X2 = 6 – X3 - X4 – X1; (6) F(x) = 28 + X3 + 4X4 + X1 + X12 + 4X5 + X6. Следовательно, мы получили базисные переменные X2, X7, X8, X9, X10, X11; свободные – X1, X3, X4, X5, X6, X12. Приравняем свободные члены к нулю и найдем базисные переменные: Если X1 = 0; X3 = 0; X4 = 0; X5 = 0; X6 = 0; X12 = 0, то из уравнений (1), (2), (3), (4), (5), (6) получим X2 = 6; X7 = 2; X8 = 6; X9 = 4; X10 =0; X11 = 6. F(x) = 28 Запишем в таблицу результат решения задачи:
Решим данную задачу методом потенциалов. Потенциалами называется система чисел, приписанных, соответственно, каждой строке i (ui) и каждому столбцу j (vj). Потенциал (ui), который устанавливается для каждой строки, можно условно принять за цену продукта в пункте его производства, потенциал (vj), который устанавливается для каждого столбца можно условно принять за цену продукта в пункте потребления. В простейшем случае цена продукта в пункте потребления равна цене продукта в пункте производства плюс транспортные расходы на его перевозку (cij). ui + cij = vj; ui = vj – cij. Шаг 1. Построение первоначального плана методом «наименьшей стоимости» (по строкам или столбцам) или методом «северо-западного угла». В первую очередь следует рассматривать строки (столбцы) с максимальными объемами производства (потребления). Искомой строкой является третья равная 10 т. В этой строке наименьшая стоимость перевозки находится на пересечении строки с первым столбцом и равна нулю. Поэтому есть возможность полностью удовлетворить потребность первого потребителя, равную 4 т, причем у третьего поставщика останется еще 6 т (10т – 4т) продукции. Заполним результат в таблицу:
Следующей по объему ресурсов является вторая строка (8т) и наименьшая стоимость перевозки находится в 4-ом столбце. Следовательно, можно полностью удовлетворить потребность четвертого потребителя (6т), а у поставщика останется 2т продукции. Аналогично распределяем продукцию первого поставщика. Минимальные затраты на перевозку имеет первый пункт потребления, который уже не нуждается в поставках. Следовательно, мы можем удовлетворить второго потребителя полностью и т.д. Первоначально составленный план перевозок должен удовлетворять условию: оптимальное решение транспортной задачи то, в котором число перевозок не превышает i +j – 1. В нашем примере i = 3; j = 4 Þ 3 + 4 – 1 = 6. Так как число перевозок (выделено жирными цифрами в левом нижнем углу квадрата) в полученном плане 5, то условие выполняется.
Шаг 2. Построение системы потенциалов, которое начинают с того, что строке 1 присваивают ноль, т.е. принимают условную цену продукта в первом пункте производства равной нулю (u1 = 0). Продукт направляют второму потребителю. Следовательно, условная цена во втором пункте потребления составит v2 = u1 + c12 = 0 + 2 = 2. Находим цену в третьем пункте производства u3 = v2 – c33 = 2 – 2 = 0. Находим цену продукта в пунктах потребления 1, 3. v1 = u3 + c31 = 0 + 0 = 0, v3 = u3 + c33 = 0 + 2 = 2. Находим цену производства во втором пункте u2 = v3 – c23 = 2 – 2 = 0. Находим цену продукта в 4 пункте потребления v4 = u2 + c24 = 0 + 0 = 0.
Шаг 3. Проверка первоначального плана на оптимальность, исходя из принципа, что при любом его изменении, т.е. при перестановке перевозок в свободные квадраты, условная цена в пунктах потребления не должна быть меньше, чем в принятом нами плане, т.е. ui + cij ³ vj. Осуществим проверку для свободных квадратов: u1 + c11 = 0 + 1 = 1 > v1 = 0, u2 + c22 = 0 + 3 = 3 > v2 = 2, u1 + c13 = 0 + 3 = 3 > v3 = 2, u3 + c32 = 0 + 2 = 2 > v2 = 2, u1 + c14 = 0 + 4 = 4 > v4 = 0, u3 + c34 = 0 + 1 = 1 > v4 = 0. u2 + c21 = 0 + 4 = 4 > v1 = 0, Условие оптимальности выполняется для всех квадратов. Затраты на транспортировку составят 4*0+6*2+2*2+6*2+6*0=28. Если условие оптимальности не выполняется, то переходят к шагу 4.
Шаг 4. Оптимизация плана. Тот квадрат, в котором не выполняется условие оптимальности, помечают точкой. Затем проводят замкнутую ломаную линию, одна из вершин которой соединена с точкой, а остальные находятся в занятых (перевозками) квадратах. Начиная с квадрата, в котором стоит точка, поочередно по часовой стрелке присваиваем квадратам с вершинами «+» и «-». Из квадрата со знаком «-» выбираем наименьшее количество продукта и перемещаем его в квадрат со знаком «+». Если план не является оптимальным одновременно для нескольких квадратов, то, в первую очередь, производится перемещение перевозок в тот квадрат, в котором условие оптимальности нарушено больше, чем во всех остальных. Для нового плана вычисляем значения потенциалов и проверяем новый вариант на оптимальность. Решение транспортной задачи в сетевой форме (без ограничения пропускной способности).
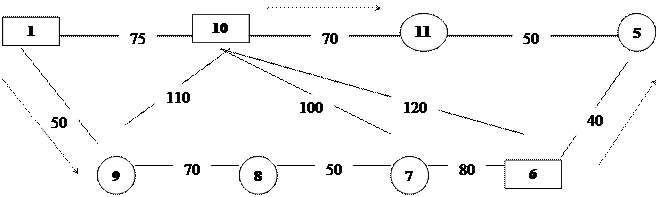
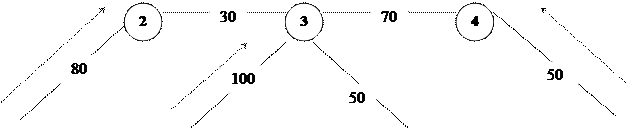
Пример 2. На рис 8. представлена сеть с 11 вершинами и 18 звеньями. В каждом звене поставлено число, характеризующее расстояние сij между соседними вершинами, соединенными данным звеном. В круглых скобках против каждой вершины отмечены размеры ресурсов со знаком «+» и потребности со знаком «-». Необходимо распределить грузопотоки таким образом, чтобы минимизировать расстояние перевозок продукции. Решим задачу, сформулированную в сетевой форме без ограничения пропускной способности.
(-80) (-120) (-150)
(+300) (+100) (-40) (-60)
(-50) (-75) (-25) (+200)
Рис.8. Исходные данные для решения транспортной задачи Решение: Шаг 1. Составляем исходный план, при котором все ресурсы поставщиков должны быть распределены между соответствующими потребителями. Стрелками показывают направления грузопотоков, а цифрами над ними – количество перевозимой продукции (рис. 9). Шаг 2. Присваиваем каждой вершине потенциалы, начиная с первой. Потенциал – это любое произвольное число, которое по размеру больше, чем максимальное расстояние между двумя вершинами (в нашем примере – больше 120). Допустим, число 200. Затем приступаем к присвоению потенциалов остальным вершинам, придерживаясь следующего правила: при продвижении по дугам в направлении следования грузопотоков к потенциалу предыдущей вершины прибавляем длину звена (расстояние между вершинами), а при движении по дугам против потока эту длину из потенциала предыдущей вершины отнимаем (рис.10). В некоторых случаях дуги с грузопотоками могут образовать два замкнутых контура, не соединенных друг с другом. В этом случае оба контура соединяют дугами с нулевыми грузопотоками, которые включают в базис для определения потенциалов вершин.

(-80) (-120) (-150)
(+300) (+100) (-40) (-60)
(-50) (-75) (-25) (+200)
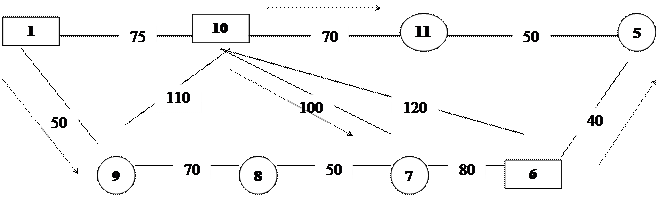
Рис.9. Направления грузопотоков плана Шаг 3. Проверяем, выполняется ли условие оптимальности на всех дугах сети, на которых нет грузопотоков, т.е. соблюдается ли условие: vj – ui £ cij. (разница потенциалов двух вершин, соединенных дугой, на которой нет грузопотока. Таких дуг в нашем примере 7. Это дуги 1-10; 9-10; 10-7; 10-6; 11-5; 3-11; 8-7). При невыполнения условия план перевозок не является оптимальным, т.к. при переводе грузопотока на данные дуги общее расстояние перевозок уменьшится. Проверим условие оптимальности на дугах: 1-10: 210-200=10 < 75; 10-6: 290-210=80< 120; 9-10: 250-210=40< 110; 11-5: 330-280=50 = 50; 10-7: 370-210=160 > 100 – не выполняется; 3-11: 310-280=30 < 50; 8-7: 370-320=50= 50.
(-80) 280 (-120) 310 (-150) 380
(+300) 200 (+100) 210 (-40) 280 (-60) 330
(-50) 250 (-75) 320 (-25) 370 (+200) 290
Рис.10. Распределение потенциалов по вершинам сети
Шаг 4. По дуге с максимальными нарушениями условия оптимальности направляем грузопоток от вершины с меньшим потенциалом до вершины с большим потенциалом (от 10 к 7) в объеме необходимой потребности (25), одновременно отнимая ее из всех встречных грузопотоков (рис. 11). Аналогично свободные от грузопотоков дуги проверяем на оптимальность: 1-10: 210-200=10 < 75; 11-5: 330-280=50 = 50; 9-10: 250-210=40< 110; 3-11: 310-280=30 < 50; 10-6: 290-210=80< 120; 8-7: 320-310=10< 50. 7-6: 310-290=20< 80; Все условия оптимальности выполняются.

(-80) 280 (-120) 310 (-150) 380
(+300) 200 (+100) 210 (-40) 280 (-60) 330
(-50) 250 (-75) 320 (-25) 370 (+200) 290
Рис.11. Направление грузопотоков плана №2 Оптимальный план перевозок на сети без ограничения пропускной способности всегда образует дерево с числом звеньев на 1 меньше, чем число вершин. Этим правилом следует руководствоваться при составлении первоначального базисного плана, который не должен содержать замкнутых контуров. В нашем примере оптимальный план перевозок изображен в виде дерева на рис. 12.
Рис.12. Оптимальный план перевозок.
|