Решение. Т.к. плоскости параллельны, то их нормальные векторы коллинеарны, т.еТ.к. плоскости параллельны, то их нормальные векторы коллинеарны, т.е. Тогда уравнение плоскости запишется:
3.2. Уравнение плоскости, проходящей Пусть плоскость проходит через 3 данные точки, не лежащие на одной прямой:
Рис. 3.2
Условие их компланарности будет векторным уравнением плоскости:
Запишем это уравнение в координатной форме, используя условие компланарности векторов, заданных в проекциях.
Задача 3.3. Записать уравнение плоскости грани
|
{–3, –4, –12} – вектор первой плоскости 
коллинеарен 
для искомой плоскости. Возьмем вектор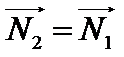 
, т.е. 
={–3, –4, –12}, т.к. коэффициент соответственных координат может равен 1.
или
.
(
), 
. Любая произвольная точка M (x, y, z) образует с данными векторы 
, 
, 
– лежащие в одной плоскости – т.е. векторы компланарны (см. рис. 3.2).
=0
пирамиды, проходящей через т. 
, если 
(2, 0, –2), 
(6, 2, –6), 
(–2, 4, –4).
