Решение. Используем уравнение прямой, проходящей через 2 точки и
Используем уравнение прямой, проходящей через 2 точки
Здесь {–4, –10, –6} – координаты направляющего вектора прямой – ребра пирамиды
Контрольные вопросы
Чем определяется угловой коэффициент прямой? Каким образом определяется расстояние от точки до плоскости? Как определить угол между двумя плоскостями? Сформулируйте условие параллельности и перпендикулярности плоскостей. Приведите вывод канонического уравнения прямой. Что такое направляющий вектор прямой?
Контрольные задания
1. Составить уравнение прямой, проходящей через точку 2. Составить уравнение прямой, проходящей через точку 3.** Составить уравнение высоты BD в треугольнике с вершинами А (7; 0), В (3; 6), С (–1; 1). 4.* Составить уравнения диагоналей ромба, заданного точками А (2; 2), В (3; 5), С (4; 2), D (3; –1). 5. Составить уравнения сторон квадрата, заданного точками А (1; 1), В (4; 2), С (5; –1), D (2; –2). 6.** Треугольник задан точками А (5; 2), В (–1; –4), С (–5; –3). Составить уравнение прямой, проходящей через точку В параллельно АС. 7. Составить уравнения прямых, заданных двумя точками:
8.* Составить уравнения сторон треугольника с вершинами А (–1; 2), В (5; 3), С (4, –2). 9.* Составить уравнения диагоналей квадрата ABCD, заданного точками А (1; 1), В (4; 2), С (5; –1), D (2; –2). 10. Указать, какая пара уравнений соответствует параллельным прямым:
11. Указать, какая пара уравнений соответствует перпендикулярным прямым:
12.** Составить уравнение высоты AD треугольника, заданного точками A (–5; 3), B (3; 7), C (4; –1).
Глава 4 ВВЕДЕНИЕ В АНАЛИЗ
4.1. Предел последовательности. Предел функции
1. Числовой последовательностью называется функция Обозначают: 2. Число а называют пределом последовательности
Обозначают: 3. Неравенство (*) равносильно неравенствам 4. Последовательности, имеющие предел, называются сходящимися; если нет предела – расходящимися. 5. Из определения предела последовательности следует, что предел постоянной равен этой постоянной:
6. Бесконечно малой последовательностью называется Для двух бесконечно малых последовательностей 1. Последовательность 2. Число b называется пределом функции Обозначение предела
Если
Пусть Отношение Если при Задача 4.1. В каких границах меняется
|

 и
и 
 ,
, 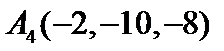
 .
. .
. = (5; 0).
= (5; 0). = (–3; 2).
= (–3; 2).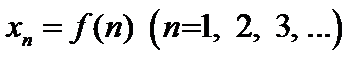 , определённая на множестве натуральных чисел. Каждое значение
, определённая на множестве натуральных чисел. Каждое значение  называется элементом последовательности, а число n – его номером.
называется элементом последовательности, а число n – его номером. или
или  .
. , если для любого
, если для любого  > 0 существует такое натуральное число N, что при всех
> 0 существует такое натуральное число N, что при всех  выполняется неравенство
выполняется неравенство (*)
(*)
 или
или 

 , предел которой равен нулю, т.е.
, предел которой равен нулю, т.е.  .
. и
и  – сумма, разность и произведение тоже является бесконечно малыми последовательностями.
– сумма, разность и произведение тоже является бесконечно малыми последовательностями. называется бесконечно большой, если для любого числа
называется бесконечно большой, если для любого числа  существует такой номер N, что при всех n > N выполняется неравенство:
существует такой номер N, что при всех n > N выполняется неравенство: 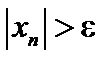 , при этом случае пишут
, при этом случае пишут 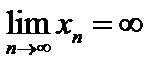 .
. при
при  , если для любого числа
, если для любого числа  существует такое
существует такое  , что при всех
, что при всех  , удовлетворяющих условию
, удовлетворяющих условию  выполняется неравенство
выполняется неравенство  .
. в точке а:
в точке а: .
. имеют конечный предел при
имеют конечный предел при  , то
, то
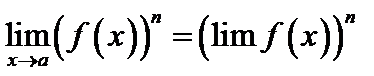


 .
. и
и  – функции, одновременно обращающиеся в ноль, при
– функции, одновременно обращающиеся в ноль, при 
 и
и  .
. теряет смысл при
теряет смысл при 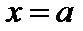 . Тогда говорят, что функция
. Тогда говорят, что функция  в точке
в точке  имеет неопределенность
имеет неопределенность  .
.  называется раскрытием неопределенности вида
называется раскрытием неопределенности вида  .
. функции
функции  и
и  стремятся к
стремятся к  , то говорят, что в точке
, то говорят, что в точке 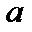 функция
функция  имеет неопределенность вида
имеет неопределенность вида  . Данная задача раскрытия неопределенности вида
. Данная задача раскрытия неопределенности вида  называется отыскания предела
называется отыскания предела  при условии, что
при условии, что  ;
;  .
. , если
, если  < 3?
< 3?


