Решение. . . .
d=
3.4. Угол между плоскостями Если даны две плоскости уравнениями:
то их нормальные векторы
Задача 3.4. Определение угла между плоскостями сводится к нахождению угла между векторами (см. рис. 3.3). Рис.3.3
Решение. Перенесем
Условие перпендикулярности двух плоскостей
3.5. Прямая в пространстве 1. Каноническое уравнение прямой (см. рис. 3.4.). Пусть прямая проходит через т. Напишем уравнение этой прямой. Для этого возьмем на ней произвольную т. M(x, y, z). Составим вектор
Рис.3.4
Этот вектор будет коллинеарен вектору
Вектор
2. Параметрическое уравнение прямой. Положим в канонических уравнениях отношения равными t – параметру
тогда получим:
Здесь Задача 3.5. Составить каноническое и параметрическое уравнение прямой, проходящей через т. M (1, 2, 3) и параллельно вектору
|
= 
= 
= 
.
(I)
, (II)
={ 
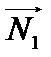} и 
={ 
}.
и 
в любую точку пространства и определим φ по скалярному произведению двух векторов
= 
.
или
, параллельности 
– const.
параллельно данному вектору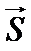 
{ m, n, p }.
={ 
}.
. По условию коллинеарности векторов можно записать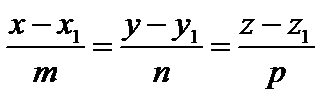
– это уравнение называется каноническим уравнением прямой в пространстве.
{ m, n, p } называется направляющим вектором этой прямой. Если 
– единичный вектор, т.е. 
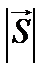=1, то 
; 
; 
, где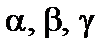 
– углы образуемые вектором 
с осями Ox; Oy; Oz.
,
, 
, 
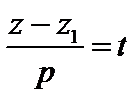или
– координаты точки 
, а m, n, p – проекции направляющего вектора 
.
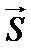{2, –7, 10}.
