Найдем расстояние между точками А и В, В и С, С и А.


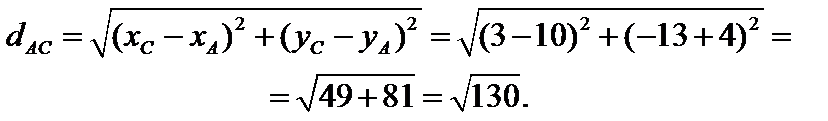
P=  +
+  +
+ 
 21, 6+11, 4+11, 4
21, 6+11, 4+11, 4  44, 4.
44, 4.
2.7. Расстояние от точки до прямой.
Вывод нормального уравнения прямой
Предположим, что в общем уравнении прямой Ах + Ву + С = 0 выполняется условие А  + В
+ В  = 1. Геометрически это означает (см. рис. 2.7).
= 1. Геометрически это означает (см. рис. 2.7).

Рис. 2.7
Если провести из начала координат на прямую вектор, то его длина равна 1 (см. рис. 2.7). Вектор  – нормальный (перпендикулярный) единичный вектор прямой, где А и В – проекции этого вектора на оси ОХ и ОУ. В этом случае уравнение называем нормальным и записывается так: А
– нормальный (перпендикулярный) единичный вектор прямой, где А и В – проекции этого вектора на оси ОХ и ОУ. В этом случае уравнение называем нормальным и записывается так: А  х + В
х + В 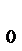 у + С
у + С  =0. Любое другое уравнение прямой (общее) приведем к нормальному виду, если разделим его левую часть на
=0. Любое другое уравнение прямой (общее) приведем к нормальному виду, если разделим его левую часть на  , тогда
, тогда  является нормирующим множителем. Иногда это уравнение записывается так:
является нормирующим множителем. Иногда это уравнение записывается так:
 или
или  , т.е.
, т.е. 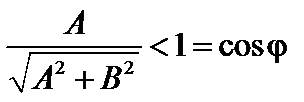
(φ – угол наклона нормального вектора к оси ОХ)
 – длина вектора
– длина вектора 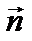
Найдем расстояние от т.  до прямой Ах + Ву + С = 0. Приведем уравнение прямой к нормальному виду. Для этого умножим на
до прямой Ах + Ву + С = 0. Приведем уравнение прямой к нормальному виду. Для этого умножим на  – нормирующий множитель. Получим
– нормирующий множитель. Получим  , подставим т.
, подставим т.  в это уравнение.
в это уравнение.
Тогда 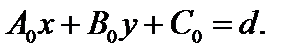
 т.к.
т.к.  для вектора
для вектора  . Вектор
. Вектор  – вектор расстояния от т.
– вектор расстояния от т.  до прямой. Длина вектора
до прямой. Длина вектора  =
=  =
=  , т.к.
, т.к.  =
=  (рис. 2.7).
(рис. 2.7).
Следовательно, 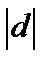 =
=  – расстояние от т. М до прямой Ах + Ву + С = 0 или
– расстояние от т. М до прямой Ах + Ву + С = 0 или  =
=  .
.
Задача № 2.7. Найти расстояние от т. М (–1; 2) до прямой 5 х + 12 у + 8 = 0.



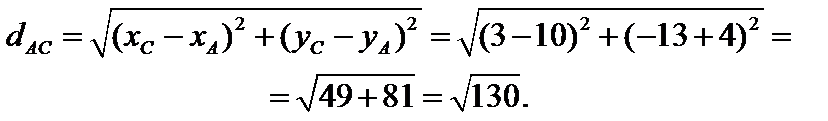
 +
+  +
+ 
 21, 6+11, 4+11, 4
21, 6+11, 4+11, 4  44, 4.
44, 4. + В
+ В  = 1. Геометрически это означает (см. рис. 2.7).
= 1. Геометрически это означает (см. рис. 2.7). – нормальный (перпендикулярный) единичный вектор прямой, где А и В – проекции этого вектора на оси ОХ и ОУ. В этом случае уравнение называем нормальным и записывается так: А
– нормальный (перпендикулярный) единичный вектор прямой, где А и В – проекции этого вектора на оси ОХ и ОУ. В этом случае уравнение называем нормальным и записывается так: А  х + В
х + В 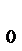 у + С
у + С  =0. Любое другое уравнение прямой (общее) приведем к нормальному виду, если разделим его левую часть на
=0. Любое другое уравнение прямой (общее) приведем к нормальному виду, если разделим его левую часть на  , тогда
, тогда  является нормирующим множителем. Иногда это уравнение записывается так:
является нормирующим множителем. Иногда это уравнение записывается так: или
или  , т.е.
, т.е. 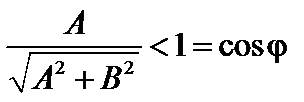
 – длина вектора
– длина вектора 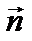
 до прямой Ах + Ву + С = 0. Приведем уравнение прямой к нормальному виду. Для этого умножим на
до прямой Ах + Ву + С = 0. Приведем уравнение прямой к нормальному виду. Для этого умножим на  – нормирующий множитель. Получим
– нормирующий множитель. Получим  , подставим т.
, подставим т.  в это уравнение.
в это уравнение.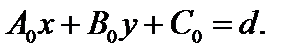
 т.к.
т.к.  для вектора
для вектора  . Вектор
. Вектор  – вектор расстояния от т.
– вектор расстояния от т.  до прямой. Длина вектора
до прямой. Длина вектора  =
=  =
=  , т.к.
, т.к.  =
=  (рис. 2.7).
(рис. 2.7).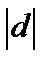 =
=  – расстояние от т. М до прямой Ах + Ву + С = 0 или
– расстояние от т. М до прямой Ах + Ву + С = 0 или  =
=  .
.


