Скалярное произведение векторов. Скалярным произведением двух векторов и называется произведение длин этих векторов на косинус угла между нимиСкалярным произведением двух векторов
Если
Рассмотрим векторы в пространстве декартовой системы координат (рис. 1.5). Выберем на осях координат единичные векторы
Рис. 1.5
Длина вектора определяется по формуле:
Можно показать, что скалярное произведение двух векторов равно сумме произведений их одноимённых координат.
если
Пример № 1.1. Найти скалярное произведение векторов. Решение.
Пример № 1.2. Между точками
|
и 
называется произведение длин этих векторов на косинус угла между ними.
, то их скалярное произведение равно 0.
, так как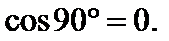 
– орты. Тогда каждый вектор определяется в этой системе через их проекции на оси OX, OY, OZ.
,
.
,
, 
, 
.
,
, 
.
, 
,
.
получили два вектора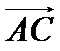 
и 
. Найти их проекции и вычислить скалярное произведение 
