Решение. Образуем векторы, лежащие в плоскости
Образуем векторы, лежащие в плоскости
Раскроем определитель
3.3. Нормальное уравнение плоскости. Аналогично тому, как выводится нормальное уравнение прямой из общего уравнения, так же получается и нормальное уравнение плоскости. По аналогии запишем:
+ или Углы a, β, γ – углы образованные нормальными векторами с осями координат. Расстояние от точки до плоскости рассчитывается по формуле: d=
Задача 3.4. Дана плоскость
|

 . Возьмем произвольную точку M (x, y, z). Тогда получаем уравнение через определитель III порядка:
. Возьмем произвольную точку M (x, y, z). Тогда получаем уравнение через определитель III порядка: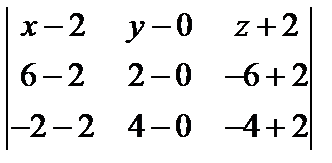 =0
=0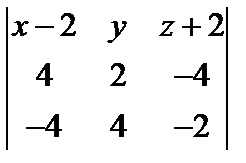 =0
=0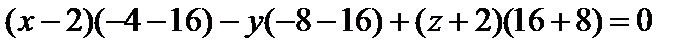
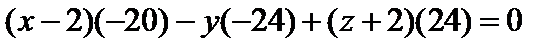 (сокращаем на –4)
(сокращаем на –4)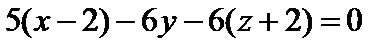

 – уравнение плоскости
– уравнение плоскости  .
. – общее уравнение плоскости, тогда нормирующий множитель: N =
– общее уравнение плоскости, тогда нормирующий множитель: N = 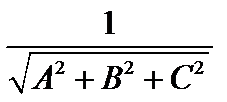 и
и x +
x +  y +
y + 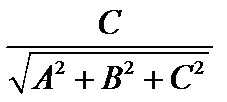 z +
z + = 0
= 0 – нормальное уравнение плоскости.
– нормальное уравнение плоскости. .
. и точка (1, 0, 0). Найти расстояние от точки до плоскости.
и точка (1, 0, 0). Найти расстояние от точки до плоскости.


