Решение. Замещаем приращение функции ее полным дифференциалом
Замещаем приращение функции ее полным дифференциалом.
Полагая, что
5.3. Дифференцирование сложных функции
Определение: Функция Z называется сложной функцией от независимых переменных x, y, …, t, если задана она через промежуточные аргументы
Частная производная сложной функции по одной из независимых переменных равна сумме произведений ее частных производных по промежуточным аргументам на частные производные этих аргументов по независимой переменной:
Если все аргументы
Задача 5.10.
Далее.
Задача 5.11. Здесь z от u и v, а сами u и v зависят от x и y. Тогда
5.4. Частные производные высших порядков Частные производные Обозначения:
Аналогично определяются производные III, IV… порядков.
Задача 5.12. Найти частные производные второго порядка
|
есть частное значение функции 
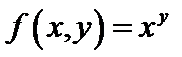в точке М 1 (1, 08; 3, 96) и что вспомогательная точка будет М 0 (1; 4), получим: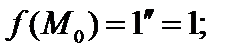
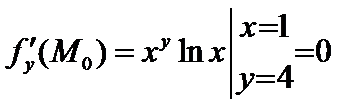, так как ln1 = 0;
; 
.
; 
;
; 
.
зависят от одной независимой переменной x, то z – сложная функция от x. Тогда производная сложной функции называется полной и вычисляется по формуле
, 
, v = cos x.
, 
, 
.
, 
первого порядка обычно зависят от тех же аргументов и каждую из них можно дифференцировать по каждому аргументу.
– смешанная частная производная.
