1.  по (1).
по (1).
2.  по (3).
по (3).
3.  по (7).
по (7).
4.  по (10).
по (10).
5.  представляет (2), где
представляет (2), где  По этой формуле
По этой формуле 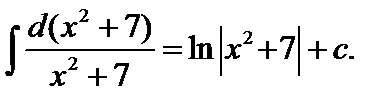
6.  – представляет формулу (5) при
– представляет формулу (5) при  . Поэтому
. Поэтому 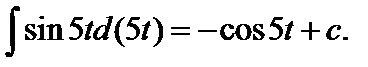
7.  т.к.
т.к.  по (4) формуле, где
по (4) формуле, где  получим
получим 
Можно проверить правильность вычисления дифференцированием.
Например.
1. 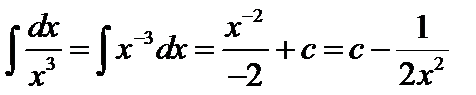 по (1)-й формуле
по (1)-й формуле
 ,
, 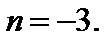
Проверка.
 – получим ….
– получим ….
2.  по (9), где u = x, a 2 = 2.
по (9), где u = x, a 2 = 2.
Проверка.
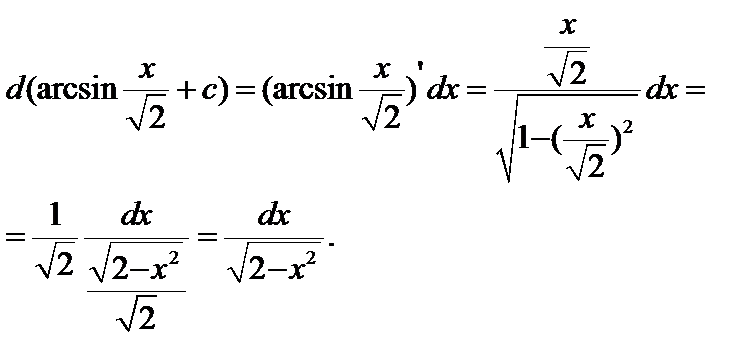

3.  , по формуле (3).
, по формуле (3).
Проверка.
 по формуле (8).
по формуле (8).
Проверка. 
6.2. Интегрирование разложением
подынтегральных функций на слагаемые
1. 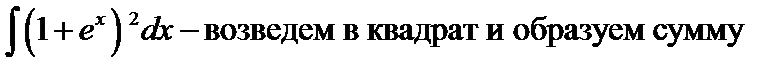
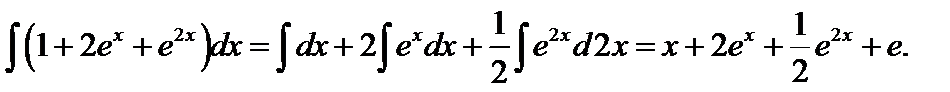
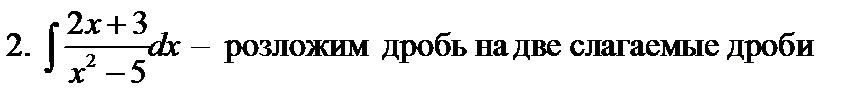
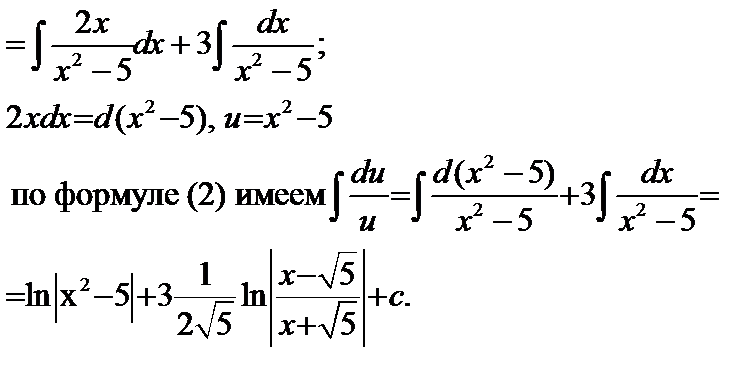
3. 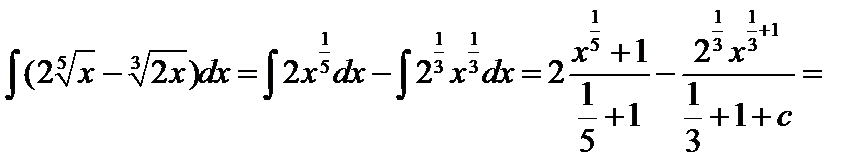
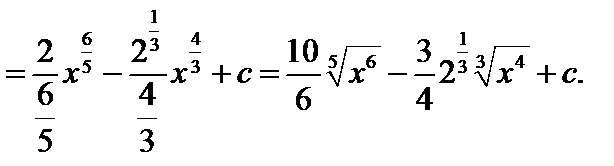
4. 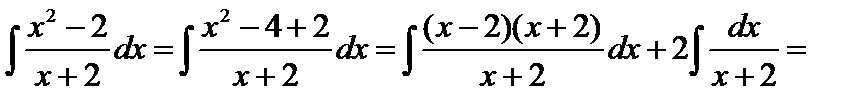

5.  – возведем в квадрат и образуем сумму
– возведем в квадрат и образуем сумму
= 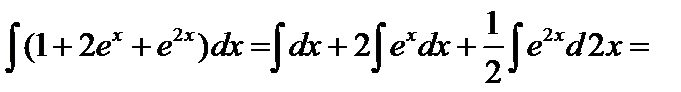

6.  – разложим дробь на две дроби
– разложим дробь на две дроби
= 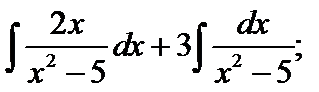
2 xdx + d (x 2–5), u = x 2 – 5 по формуле (2) имеем
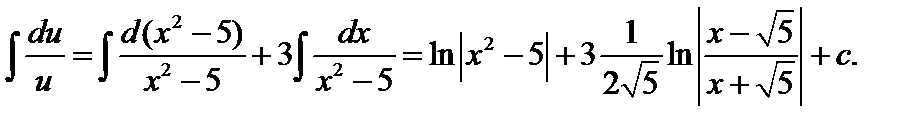
7. 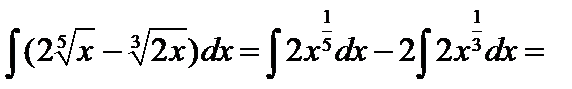

8. 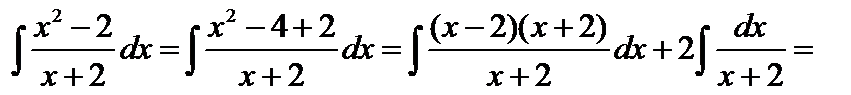
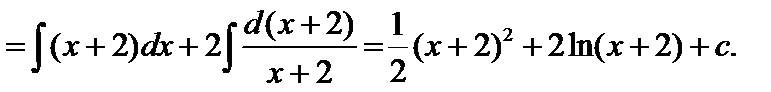
6.3. Интегрирование посредством замены
переменной
Для нахождения интеграла  можно заменить переменную x переменной t, связанной формулой x = φ (t), dx = φ ′ (t) dt и получим
можно заменить переменную x переменной t, связанной формулой x = φ (t), dx = φ ′ (t) dt и получим  – полученный интеграл преобразуем к переменной х
– полученный интеграл преобразуем к переменной х

 по (1).
по (1). по (3).
по (3). по (7).
по (7). по (10).
по (10). представляет (2), где
представляет (2), где  По этой формуле
По этой формуле 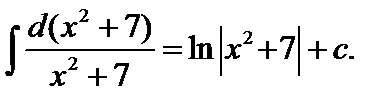
 – представляет формулу (5) при
– представляет формулу (5) при  . Поэтому
. Поэтому 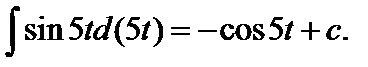
 т.к.
т.к.  по (4) формуле, где
по (4) формуле, где  получим
получим 
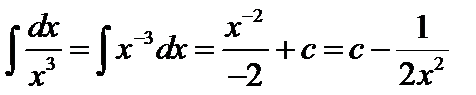 по (1)-й формуле
по (1)-й формуле ,
, 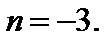
 – получим ….
– получим …. по (9), где u = x, a 2 = 2.
по (9), где u = x, a 2 = 2.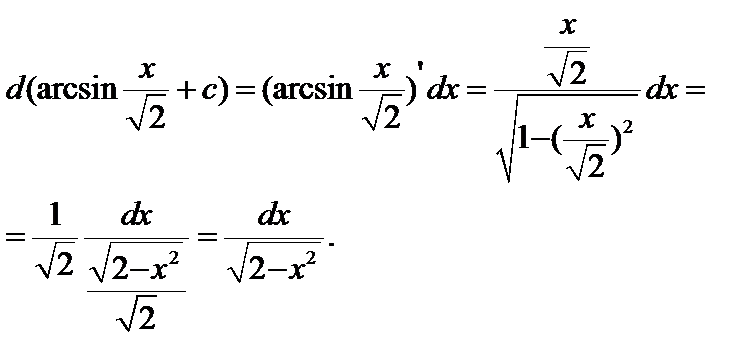

 , по формуле (3).
, по формуле (3). по формуле (8).
по формуле (8).
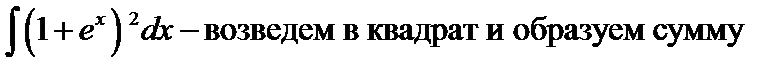
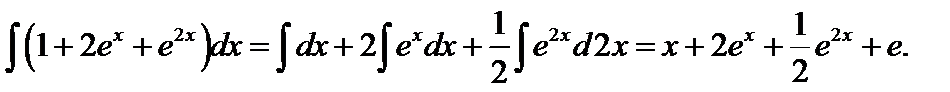
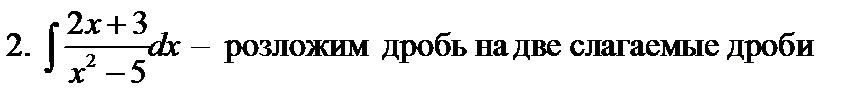
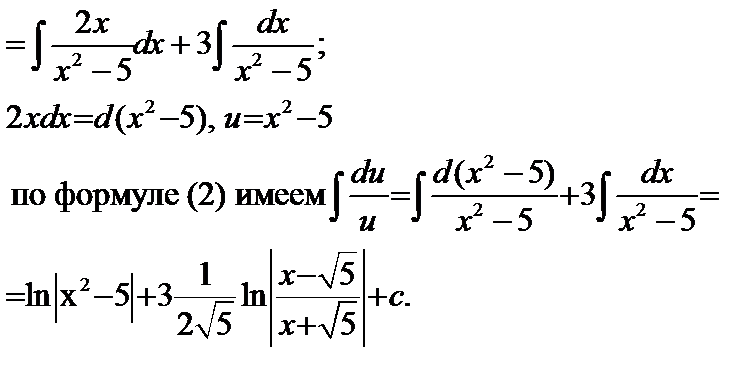
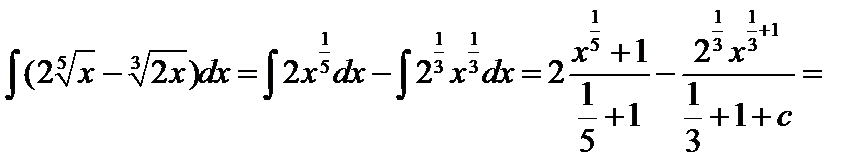
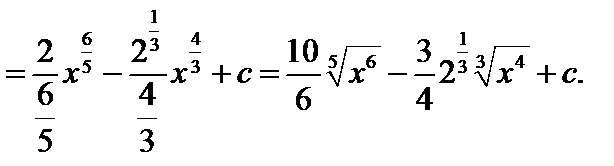
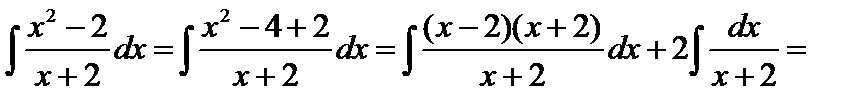

 – возведем в квадрат и образуем сумму
– возведем в квадрат и образуем сумму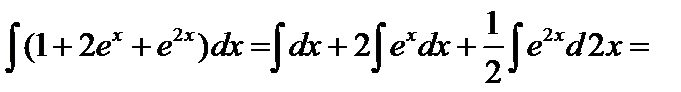

 – разложим дробь на две дроби
– разложим дробь на две дроби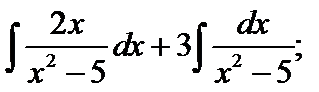
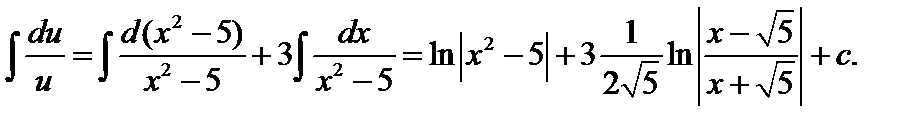
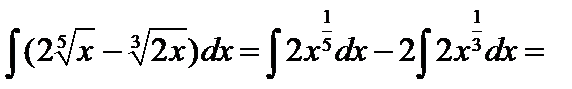

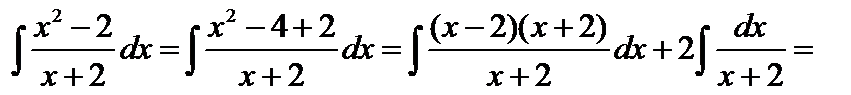
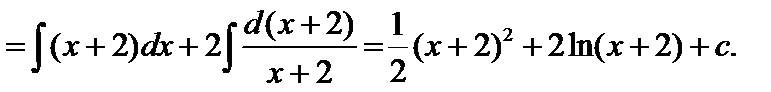
 можно заменить переменную x переменной t, связанной формулой x = φ (t), dx = φ ′ (t) dt и получим
можно заменить переменную x переменной t, связанной формулой x = φ (t), dx = φ ′ (t) dt и получим  – полученный интеграл преобразуем к переменной х
– полученный интеграл преобразуем к переменной х


