Примеры на различные типы
1.
2.
3.
a. первый интеграл
b. второй интеграл берём как от нечётной степени
Окончательно:
4.
(выделим целую часть от неправильной дроби)
5.
6.
7.
8.
Контрольные задания 1. Вычислить неопределенные интегралы и проверить результаты дифференцированием:
2. Вычислить неопределенные интегралы и проверить результаты дифференцированием:
3. Найти неопределенные интегралы
Раздел 7 ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
7.1. Формула Ньютона-Лейбница Определённым интегралом называется предел интегральной суммы
Обозначается Вычислять определённый интеграл нужно с помощью неопределённого интегрирования. Если F (x) есть любая первообразная функции f (x) т.е.
Определённый интеграл равен разности значений неопределённого интеграла при верхнем и нижнем пределах интегрирования.
|














 т.к.
т.к. =
=


 применяя универсальную тригонометрическую подстановку
применяя универсальную тригонометрическую подстановку 















 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f.
;
f.  ;
g.
;
g.  ;
h.
;
h.  ;
i.
;
i.  ;
;
 ;
k.
;
k.  ;
l.
;
l.  ;
m. *
;
m. *  ;
n.
;
n.  ;
o.
;
o.  ;
p.
;
p.  ;
q.
;
q.  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f.
;
f.  ;
g.
;
g.  ;
h. **
;
h. ** 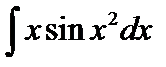 ;
i.
;
i.  ;
j. *
;
j. *  ;
k.
;
k.  ;
;
 ;
m. *
;
m. *  ;
n. *
;
n. *  ;
o.
;
o.  ;
p.
;
p.  ;
q. *
;
q. *  ;
r. **
;
r. **  ;
s. **
;
s. **  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f. *
;
f. *  ;
g.
;
g.  ;
h.
;
h.  ;
i. *
;
i. *  ;
;
 ;
k. *
;
k. *  ;
l.
;
l.  ;
m. **
;
m. **  ;
n. **
;
n. **  ;
o.
;
o.  ;
p. **
;
p. **  .
.
 , при условии, что число промежуточных точек неограниченно возрастает, а длина частных сегментов (отрезков)
, при условии, что число промежуточных точек неограниченно возрастает, а длина частных сегментов (отрезков)  стремится к 0.
стремится к 0.

 .
. (x) = f (x), то интеграл
(x) = f (x), то интеграл (1) – формула Ньютона-Лейбница.
(1) – формула Ньютона-Лейбница.


