Решение. Решая систему получаем М1(0, 0) и М2(1, 1/2) обе точки критические, т.к Z определена на
Решая систему получаем М 1(0, 0) и М 2(1, 1/2) обе точки критические, т.к Z определена на всей OXY. Исследуем критические точки
Для М 1(0, 0) = А = 0, В = –6, С =0, ∆ (М 1)= АС – В 2 < 0. М 2(1, Zmin = Z(M 2) = 4.
5.6. Применение производной
План исследования: 1. Область определения функции, область значения, четность-нечетность, интервалы знаки постоянства, точки пересечения с осями координат. 2. Точки разрыва функции. 3. Интервалы возрастания, убывания, экстремумы. 4. Интервалы вогнутости, выпуклости, точки перегиба. 5. Асимптоты графика функции. 6. Построение графика. Задача 5.16. Исследовать функцию, начертить её график
1. a. функция определена всюду, кроме b. область значения c. d. точки пересечения с осями. Если x = 0, y = 0 т. М (0; 0). e. интервалы знакопостоянства
2. Точки разрыва. В точках Условие непрерывности: функция определена в х 0.
Вычисляем пределы слева и справа при стремлении к х 0. В нашем случае
слева
Замечание. Разрыв I рода, когда и/или слева, справа пределы конечные, но неравные. Например (рис. 5.2). Рис.5.2 Разрыв II рода будет в нашем случае и при Схематично (рис. 5.3). Рис. 5.3 3. Интервалы возрастания и убывания. Точки экстремума
4. Интервалы выпуклости, вогнутости, т. перегиба.
Интервалы выпуклости, вогнутости
В интервале При Точка перегиба
5. Найти асимптоты графика а. вертикальные асимптоты (рис. 5.4)
Рис. 5.4 Если b. Наклонная асимптота ищется по формуле
Если пределы существуют и конечны, то функция имеет наклонную асимптоту. В нашем примере
Уравнение асимптоты Вертикальные асимптоты бывают в точках разрыва
6. Строим график (рис. 5.5).
Рис. 5.5 Контрольные вопросы Что называется частным дифференциалом функции? Что такое полный дифференциал функции нескольких переменных? Чему равна частная производная функции нескольких аргументов? Сформулируйте необходимое условие существования экстремума функции. Приведите план исследования функции.
Контрольные задания 1. Найти производные следующих функций:
2. Найти производные следующих функций:
3. Найти производные следующих функций:
4. Найти производные следующих сложных функций:
5. Найти производные следующих сложных функций:
6. Исследовать функции и построить их графики:
Глава 6 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
6.1. Свойства неопределенного интеграла.
Описание функции Всякая непрерывная функция Неопределенный интеграл – это совокупность всех первообразных от функции
|


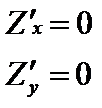
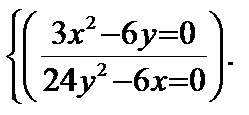
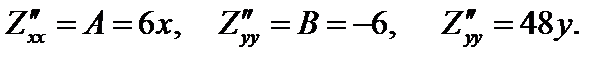
 = А = 6, В = –6, С = 24, ∆ (М 2) > 0.
= А = 6, В = –6, С = 24, ∆ (М 2) > 0.


 – четная => график функции симметричен относительно начала координат.
– четная => график функции симметричен относительно начала координат.



 функция неопределенна => в точках может быть разрыв.
функция неопределенна => в точках может быть разрыв. , где х 0 – точки на оси Ох.
, где х 0 – точки на оси Ох.

 Слева и справа пределы бесконечные – это говорит о том, что здесь разрыв II рода.
Слева и справа пределы бесконечные – это говорит о том, что здесь разрыв II рода.
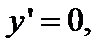













 ;
;  – max условие точки перегиба.
– max условие точки перегиба.
 , т.
, т.  – точка, подозреваемая на перегиб.
– точка, подозреваемая на перегиб.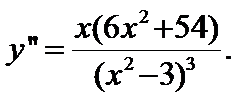

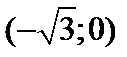






 , функция имеет выпуклый характер.
, функция имеет выпуклый характер. – вогнута.
– вогнута. , т. к. здесь меняется знак
, т. к. здесь меняется знак с + на –, точки
с + на –, точки  – точки разрыва графика функции.
– точки разрыва графика функции. , то
, то 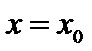 вертикальная асимптота.
вертикальная асимптота. , где
, где 





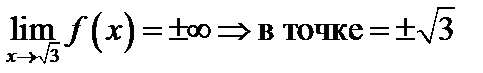 – вертикальная асимптота.
– вертикальная асимптота. ;
d.
;
d.  ;
e.
;
e.  ;
;
 ;
g.
;
g.  ;
h.
;
h.  ;
;
 ;
j. *
;
j. *  ;
k. *
;
k. *  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
;
 ;
e.
;
e.  ;
f.
;
f.  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
d. *
;
d. * 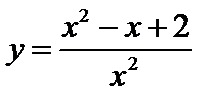 ;
;
 ;
f.
;
f.  ;
g.
;
g.  ;
h.
;
h.  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
d. *
;
d. *  ;
e.
;
e.  ;
;
 ;
g. **
;
g. **  ;
h. **
;
h. **  ;
i.
;
i.  ;
j.
;
j.  .
.
 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f.
;
f. 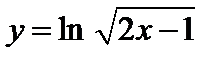 ;
g.
;
g.  ;
h.
;
h.  ;
i.
;
i.  ;
j.
;
j. 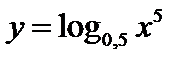 ;
k.
;
k.  ;
l. *
;
l. *  ;
m. *
;
m. *  ;
;
 ;
o.
;
o.  ;
p. **
;
p. **  ;
q.
;
q.  ;
r.
;
r.  ;
s.
;
s.  ;
t. **
;
t. **  ;
u.
;
u.  ;
v.
;
v.  ;
w.
;
w.  ;
x. **
;
x. ** 
 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f.
;
f.  ;
g.
;
g.  ;
;
 ;
i. *
;
i. *  ;
j. **
;
j. **  ;
k. **
;
k. ** 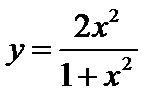 ;
l. *
;
l. *  .
.
 по известному дифференциалу
по известному дифференциалу  , т.е. действие обратное дифференцированию называется интегрированием, а исконная функция
, т.е. действие обратное дифференцированию называется интегрированием, а исконная функция  называется первообразной функцией от
называется первообразной функцией от  .
. меняет бесчисленное множество различных первообразных, которое отличается постоянным слагаемым; если
меняет бесчисленное множество различных первообразных, которое отличается постоянным слагаемым; если  есть первообразная от
есть первообразная от  , то
, то  , где
, где  – произвольная постоянная, также первообразная от
– произвольная постоянная, также первообразная от  , так как
, так как 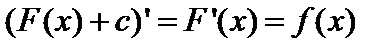 .
. и обозначается
и обозначается  ,
,  , если
, если 



