ОпределениеЧастным дифференциалом функции Обозначение Из определения частных производных следует, что
Полный дифференциал du функции u равен сумме всех ее частных дифференциалов.
Задача 5.7. Найти полные дифференциалы функций: 1. 2. Решение 1. 1. Находим частные производные 2.Умножая частные производные на дифференциалы соответствующих аргументов, получим частные дифференциалы.
Полный дифференциал найдем как сумму её частных дифференциалов
Решение 2.
Задача 5.8. Вычислить значение полного дифференциала функции.
Решение. Находим частные производные.
Подставим значения переменных x, y, dy, dx; получим, что полный дифференциал
Задача 5.9. Вычислить приближенно
|
по x называется главная часть частного приращения 
.
.
.
; 
.
.
; 
; 
;
; 
;
;
.
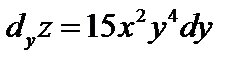, при х = 1, y = 3, dx = 0, 01, dy = –0, 05.
; 
.
.
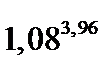