Решение. Движущаяся точка описывает одну арку циклоиды, когда t меняется от 0 до 2π, х при этом меняется от 0 до 2πa
Движущаяся точка описывает одну арку циклоиды, когда t меняется от 0 до 2π, х при этом меняется от 0 до 2π a Т.к. x = a (t – sin t), то dx = a (t – sin t)t' dt = a (1– cos t) dt.
Следовательно
Контрольные задания 1. Вычислить объём тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной линиями: 1. 2 у 2 = х 3, х = 4 [32π ]; 2. у 2 = 2 рх, х = р [π p 3]; 3. y = sin x, y = 0 (1 полуволна) [π 2/2].
2. Вычислить объём тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями 1. y 3 = 4 x 2, y = 2 [π ]; 2. x 2 + y 4 = y 2 [π p3]; 3. y = x 3, x = 0, y = 8 [19, 2π ].
3. Вычислить определенные интегралы, используя определение и их свойства:
4. Вычислить определенные интегралы, используя определение, их свойства и метод подстановки:
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ 1. Бермант, А.Ф. Краткий курс математического анализа/А.Ф. Бермант, И.Г. Аранович - М: Наука, 1969.-202с. 2. Бугров, Я.С., Высшая математика/Я.С. Бугров., С.М. Никольский: -М.: Дрофа, 2003. -198с.- ISBN 5-222-00222-5. 3. Булдык, Г.М. Сборник задач и упражнений по высшей математике/Г.М. Булдык. -Минск: ООО «Юнипресс», 2002.-231с.- ISBN 5-222-00222-5. 4. Выгодский, М.Я. Справочник по высшей математике/М.Я. Выгодский.- М: ДЖАНГАР, Большая медведица, 2001.-178с.- ISBN: 5-7102-0197-9 5. Грес, П.В. Математика для гуманитариев/П.В. Грес-М.: ЮРАЙТ, 2000.-256с.- ISBN 5-222-00222-5. 6. Гусак, А.А. Справочное пособие к решению задач по математике/А.А.Гусак.-Минск: 1998.-272с. 7. Дубровин Н.И. Задания к типовым расчетам по высшей математике/Н.И. Дубровин. Изд-во ВПИ, Владимир, 1993.-45с. 8. Ефимов, В.А. Сборник задач по математике для втузов/В.А. Ефимов, Б.П. Демидович.-М.: Наука, 1981.-165с. 9. Клиот-Дашинский, М.И. Алгебра матриц и векторов/М.И. Клиот-Дашинский.-СПб.: Лань, 2001.-189с.- ISBN 5-222-00222-5. 10. Курош, А.Г. Курс высшей алгебры/ А.Г.Курош.-М.: ГИФМЛ, 1962.-220с. 11. Максимов, Ю.Д. Курс высшей алгебры для гуманитарных специальностей/ Ю.Д. Максимов.-СПб.- Специальная литература, 1999.-178с. 12. Марков, Л.Н. Высшая математика: часть1. Элементы линейной и векторной алгебры. Основы аналитической геометрии/Л.Н.Марков, Г.П.Размыслович.-Минск: Амалфея, 1999.-167. 13. Мышкис, А.Д. Лекции по высшей математике/ А.Д. Мышкис.М.: Наука, -1969.-150с. 14. Немыцкий, В.А. Курс математического анализа/ В.А. Немыцкий.-М.: ГИТТЛ, 1957.-254с. 15. Общая алгебра/Под общ. Редакцией Л.А. Скорнякова. М.: Наука, 1990.-154с. 16. Пискунов, Н.С. Дифференциальное и интегральное исчисление/ Н.С. Пискунов. М.: Наука, 1964.-233с. 17. Подольский, В.А. Сборник задач по высшей математике/ В.А. Подольский, А.М. Суходольский. М.: Высшая школа, 1974-134с. 18. Подольский, В.А.Сборник задач по высшей математике/*В.А. Подольский, А.М. Суходский. М.: 1974Высшая школа, 1974.-134с.
|






 ;
b.
;
b. 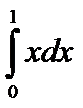 ;
c.
;
c.  ;
d.
;
d.  ;
e.
;
e.  ;
f.
;
f.  ;
g.
;
g.  ;
h.
;
h.  ;
i.
;
i. 
 ;
l.
;
l.  ;
m.
;
m. 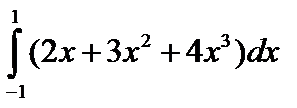 ;
n.
;
n.  ;
o.
;
o.  ;
p.
;
p.  ;
q. **
;
q. **  ;
r. *
;
r. *  ;
s. *
;
s. * 
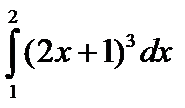 ;
b.
;
b.  ;
c.
;
c.  ;
d.
;
d.  ;
e. *
;
e. * 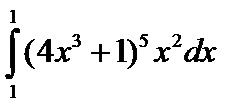 f. *
f. *  ;
g. *
;
g. *  ;
h.
;
h.  ;
;
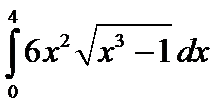 ;
j. *
;
j. * 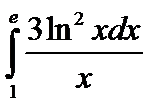 k. *
k. *  ;
l. **
;
l. **  ;
m.
;
m.  ;
n. **
;
n. **  ;
o. *
;
o. * 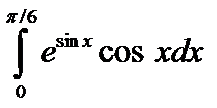 .
.



