ЗАДАЧА 4. Величина спроса на фрукты задана уравнением QD = 20 – 2P, величина предложения QS = 2 + P

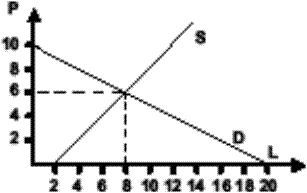
Величина спроса на фрукты задана уравнением Q_D = 20 – 2 P, величина предложения Q_S = 2 + P.

1) Определите равновесную цену и объём продаж аналитически, по графику и по таблице.

2) На основе данной функции спроса определите, как изменяется эластичность спроса при снижении цены – по показателю общей выручки.

3) Определите, достигается ли при данном равновесном количестве максимальная выручка?

4) Как изменится выручка продавца, если предложение возрастет на 3 единицы? на 5 единиц?

5) Рассчитайте эластичность спроса по коэффициенту эластичности (дуговой и точечной).

Решение. 1) Равновесная цена – цена, уравновешивающая спрос и предложение в результате действия конкурентных сил. В условиях равновесия величина спроса равна величине предложения, цена спроса равна цене предложения. Для аналитического решения приравняем функцию спроса и функцию предложения и найдем равновесную цену:

Q_D = Q_S 20 – 2 P = 2 + P 20 – 2 = 2 Р + Р

18 = 3 P

Р = 6 рублей.

Подставим значение цены в функцию спроса или в функцию предложения и определим равновесное количество Q_D = Q_S = 8 единиц.

Графически равновесие – это точка пересечения графиков спроса и предложения. Отметим по вертикальной оси значения цены, по горизонтальной оси – количество продукции и построим графики спроса и предложения по данным линейным функциям. График спроса будет выглядеть как прямая нисходящая линия. Крайние точки – это цена P = 10, при которой величина спроса Q_D = 0, и количество Q_D = 20 при цене P = 0. Кроме того, отмечаем точку равновесия P = 6, Q_D = 8. График предложения выглядит как прямая восходящая линия. Для построения отмечаем точку на горизонтальной оси – величину предложения Q_S = 2 при цене P = 0 и равновесную точку P = 6, Q_S = 8. Графики пересекаются в точке равновесия.

 

 

Рис. 17 Рыночное равновесие

Для решения в табличной форме необходимо заполнить таблицу, отмечая в ней изменение величины спроса Q_D и величины предложения Q_S при изменении (снижении) цены. В таблице принято указывать изменение цены, начиная от максимальной до P = 0. Максимально высокая цена – это цена, при которой величина спроса Q_D = 0. Соответственно, при нулевой цене величина спроса максимальна. По функции спроса находим, что величина спроса Q_D = 0, когда P = 10. Далее, на каждую единицу снижения цены величина спроса возрастает на 2 единицы, в соответствии с коэффициентом при независимой переменной (цене). При цене P = 0 величина спроса Q_D = 20 (max). Величина предложения при снижении цены на одну единицу снижается с учетом коэффициента, данного в функции, также на одну единицу.

При цене P = 6 руб. установится равновесие, то есть величина спроса равна величине предложения Q_D = Q_S = 8 единиц.

 

Цена P, руб.	Величина спроса QD, ед.	Величина предложения QS ед.	Величина предложения	Общая выручка TR = P . Q	Коэффициент эластичности спроса ED
QS +3 ед.	QS +6 ед.	∆ Q %/ ∆ P %	∆ Q/∆ P . P / Q
							∞
						5, 7	...
						...	...
6	8	8				1, 85	1, 5
						1, 2
						0, 8	...
						...	...
						...	...
						...	0, 1
						0, 05

 

2) Эластичность спроса – степень реакции потребителей на изменение цены.Эластичность спроса при линейной функции спроса не остается постоянной величиной. При последовательном снижении цены и движении по графику спроса вниз, эластичность спроса снижается, спрос из эластичного превращается в неэластичный.

Эластичность спроса можно определить по общей выручке TR = P ^. Q. Если при снижении цены TR растет, то спрос эластичный, снижать цену и увеличивать производство выгодно. Если при снижении цены TR снижается, то спрос неэластичный. Внесем показатели общей выручки TR в таблицу.

3) По таблице видно, что равновесие достигается на участке эластичного спроса, но выручка при данной функции спроса TR = P ^. Q = 6 ^. 8 = 48 не максимальна, то есть возможно дальнейшее снижение цены.

4) Если под влиянием неценовых факторов предложение возрастет на 3 единицы, функция предложения будет иметь вид Q_S = 5 + P и сместится по горизонтали на 3 единицы вниз вправо. Новые значения величины предложения внесем в таблицу. Определим новое равновесие аналитически и по таблице. В результате действия рыночного механизма цена снизится до 5 руб., объём продаж составит 10 ед., выручка TR = P ^. Q = 5 ^. 10 = 50 возрастет и будет максимальна. Если предложение возрастет на 6ед., цена снизится до 4 руб., но выручка TR = P ^. Q = 4 ^. 6 = 48 сократится, поскольку спрос стал неэластичным.

Объём, при котором выручка максимальна, можно определить аналитически. Известно, что в точке экстремума (минимальных или максимальных значений функции) производная от этой функции равна нулю. На основе функции спроса можно составить функцию общей выручки TR = P ^. Q_D. Преобразуем функцию спроса в функцию цены, то есть Q_D = 20 – 2 P, отсюда P = 10 – 0, 5 Q_D.

Тогда общая выручка TR = (10 – 0, 5 Q_D) ^. Q_D = 10 Q_D – 0, 5 Q_D ².

В точке максимума производная выручки TR΄ = MR = 0.

TR ΄ = (10 Q_D – 0, 5 Q_D ²)΄ = 10 – Q_D = 0. Отсюда Q_D = 10, соответственно P = 5.

При объёме 10 ед. и цене 5 руб. выручка достигает максимального значения, соответственно коэффициент эластичности при этом объёме будет равен E_D = 1. Дальнейшее снижение цены приведет к снижению выручки, а значит, спрос станет неэластичным, и коэффициент эластичности будет меньше единицы.

5) Эластичность спроса можно определить по коэффициенту эластичности. Обычно для расчёта используется коэффициент дуговой эластичности, который применим к небольшим интервалам изменения цены и количества:

 

;

где ∆ Q (%) – относительное изменение объёма спроса;

∆ P (%) – относительное изменение цены товара.

В этой формуле в качестве основания берется либо первое, либо второе значение цены и количества.

Более точным является расчёт коэффициента эластичности по методу центральной точки, где за основание берем среднюю величину количества и среднюю величину цены:

, или после преобразований:

, или ;

Например, при снижении цены:

– от10 руб. до 9 руб.:

E_D = (2 – 0)/(2 + 0) ^. (10 + 9)/(10 – 9) = 1 ^. 19 = 19 > 1 – эластичный спрос. → ∞

– от 9 руб. до 8 руб.:

E_D = (4 – 2)/(4 + 2) ^. (9 + 8)/(9 – 8) = 1/3 ^. 17/1 = 5, 7 > 1 – эластичный спрос. → ∞

– от 7 руб. до 6 руб.:

E_D = (8 – 6)/(8 + 6) ^. (7+6)/(7 – 6) = 1/7 ^. 13/1 = 1, 85 > 1– эластичный спрос.

– от 6 руб. до 5 руб.:

E_D = (10 – 8)/(10 + 8) ^. (6+5)/(6 – 5) = 1/9 ^. 11/1 = 1, 2 → 1 – единичная эластичность.

– от 5 руб. до 4 руб.:

E_D = (12 – 10)/(12+10) ^. (5+4)/(5 – 4) = 1/11 ^. 9/1 = 0, 8 < 1 –неэластичный спрос.

– от 1 руб. до 0 руб.:

E_D = (20 – 18)/(20 + 18) ^. (1 + 0)/(1 – 0) = 1/19 ^. 1 = 0, 05 → 0 абсолютно неэластичный спрос.

 

Если график спроса задается линейной функцией Q_D = a – bP, то можно определить эластичность спроса в каждой точке на графике, то есть при каждом сочетании цены и количества, применяя коэффициент точечнойэластичности. Коэффициент выводится из предыдущей формулы:

;

Показатель –b при независимой переменной (цене) характеризует наклон графика спроса, совпадающий с наклоном касательной во всех точках на кривой спроса и равен -b = ∆ Q/∆ P. Поэтому в формуле эластичности показатель ∆ Q/∆ P можно заменить на –b, заданный в функции спроса. Тогда формула для расчёта точечной эластичности имеет вид:

;

где b – наклон кривой спроса.

В нашем примере в функции спроса Q_D = 20 – 2 P наклон равен ∆ Q/∆ P = – 2, коэффициент точечной эластичности

;

нак «минус» говорит только об обратной зависимости между величиной спроса и ценой, поэтому при расчётах коэффициента его игнорируют.

Посчитаем коэффициент точечной эластичности:

 

P = 10, Q = 0:

E_D = 2 ^. 10/0 = ∞ – эластичный спрос;

P = 9, Q = 2:

E_D = 2 ^. 9/2 = 9 > 1 – эластичный спрос;

P = 6, Q = 8:

E_D = 2 ^. 6/8 = 1, 5 > 1 – эластичный спрос;

P = 5, Q = 10:

E_D = 2 ^. 5/10 = 1 – единичная эластичность.

P = 1, Q = 18:

E_D = 2 ^. 1/18 = 0, 1 < 1 – неэластичный спрос.

P = 0, Q = 20:

E_D = 2 ^. 0/20 = 0 – абсолютно неэластичный спрос.

 

Коэффициент точечной эластичности выражает такую же динамику изменения выручки и эластичности спроса, что и коэффициент дуговой эластичности.