Устойчивость продольно сжатых стержней
Основные понятия и формулы Выполнение условий прочности и жесткости продольно сжатых стержней не всегда гарантирует их надежность при эксплуатации. Если на длинный стержень малого поперечного сечения действует центрально приложенная продольная сжимающая сила, то при малых ее значениях стержень испытывает состояние чистого сжатия и сохраняет прямолинейную форму устойчивого равновесия. Способность сжатого стержня сохранять приданную ему при изготовлении первоначальную форму устойчивого равновесия называется устойчивостью. Рисунок 7. а При увеличении сжимающей силы до некоторого значения
происходит потеря первоначальной формы устойчивого равновесия сжатого стержня, называется критической силой. Достижение сжимающей силы критического значения приводит к разрушению элемента или конструкции в целом. Происходит оно внезапно от изгиба при значениях сжимающих напряжений, при которых прочность элемента на чистое сжатие еще не исчерпана. Потеря устойчивости одним из элементов конструкции называется местной потерей устойчивости и не обязательно приводит к разрушению всей конструкции Потеря устойчивости несколькими или всеми элементами конструкции называется общей потерей устойчивости и, как правило, приводит к разрушению всей конструкции. В пределах упругих деформаций величина критической силы определяется по формуле Л.Эйлера где
При этом в сечениях стержня действуют сжимающие критические напряжения, определяемые по формуле где
А - площадь поперечного сечения стержня. С увеличением гибкости увеличивается способность стержня к потере устойчивости. Величина критической силы и критического напряжения в пределах упругих деформаций зависит от изгибной жесткости стержня, его длины и способа закрепления концов. Влияние способа закрепления концов стержней на величину коэффициента приведения длины стержня показано на рисунке 7.2.
Рисунок 7.2 Если стержень имеет одинаковый способ закрепления концов в обеих главных плоскостях, то он теряет устойчивость в плоскости минимальной жесткости с Формулы Л.Эйлера для
За пределом пропорциональности при упруго-пластических деформациях материалов критические напряжения определяются по эмпирическим формулам Ф.С. Ясинского. Для пластичных материалов где Пределы применимости формулы Ф.С.Ясинского для пластичных материалов от предела пропорциональности
Рисунок 7.3 Для стержней малой гибкости при Величина критической силы для стержней средней и малой гибкости определяется по формуле Для обеспечения устойчивости необходимо чтобы значение продольной сжимающей силы было меньше критической Коэффициент запаса устойчивости записывается также через напряжения Величина допускаемого напряжения при расчетах на устойчивость выражается через допускаемое напряжение на сжатие. где Окончательно условие прочности при расчетах на устойчивость (условие устойчивости) записывается формулой По условию устойчивости решаются 3 задачи. Проектировочная задача определения размеров сечения Проверочная задача определения допускаемой величины продольной сжимающей силы Проверочная задача проверки устойчивости и определения коэффициента запаса устойчивости При этом расчеты на устойчивость проводятся для стоек из конструкционных материалов.
|

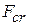 стержень изогнется и прямолинейная форма равновесия переходит в новую криволинейную форму равновесия.
стержень изогнется и прямолинейная форма равновесия переходит в новую криволинейную форму равновесия.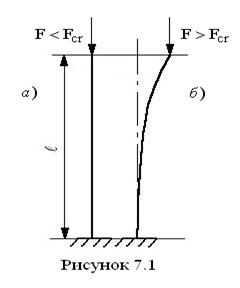 Потеря первоначальной формы устойчивого равновесия под действием продольной сжимающей нагрузки называется потерей устойчивости. Рисунок 7.1 б. При потере устойчивости стержень изгибается по уравнению синусоиды
Потеря первоначальной формы устойчивого равновесия под действием продольной сжимающей нагрузки называется потерей устойчивости. Рисунок 7.1 б. При потере устойчивости стержень изгибается по уравнению синусоиды 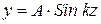 . Минимальное значение продольной сжимающей силы, при котором
. Минимальное значение продольной сжимающей силы, при котором
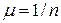 - коэффициент проведения длины стержня, показывает во сколько раз необходимо изменить длину шарнирно закрепленного по концам стержня, чтобы критическая сила для него была равна критической силе для стержня при заданных способах его закрепления.
- коэффициент проведения длины стержня, показывает во сколько раз необходимо изменить длину шарнирно закрепленного по концам стержня, чтобы критическая сила для него была равна критической силе для стержня при заданных способах его закрепления. число полуволн синусоиды изогнутой оси стержня, потерявшего устойчивость;
число полуволн синусоиды изогнутой оси стержня, потерявшего устойчивость;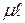 - приведенная длина стержня.
- приведенная длина стержня.
 - геометрическая гибкость стержня, характеризует способность стержня к потере устойчивости в зависимости от соотношения его продольных и поперечных размеров и способа закрепления концов;
- геометрическая гибкость стержня, характеризует способность стержня к потере устойчивости в зависимости от соотношения его продольных и поперечных размеров и способа закрепления концов; - радиус инерции сечения стержня;
- радиус инерции сечения стержня;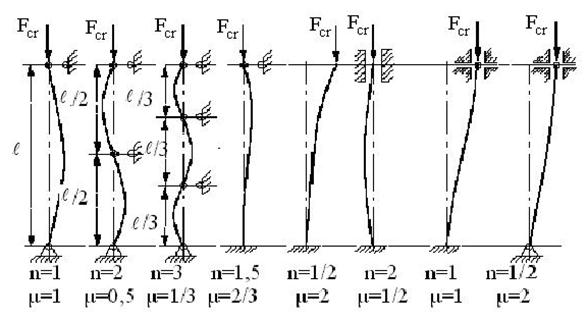
 и тогда
и тогда 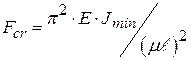 .
. справедливы при величине критических напряжений до предела пропорциональности
справедливы при величине критических напряжений до предела пропорциональности  . Пределы ее применимости по гибкости стержней
. Пределы ее применимости по гибкости стержней 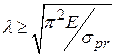 , т.е. для стержней большой гибкости. Рисунок 7.3
, т.е. для стержней большой гибкости. Рисунок 7.3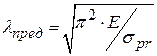 - минимальная гибкость стержня, при которой
- минимальная гибкость стержня, при которой  , называется первой предельной гибкостью.
, называется первой предельной гибкостью.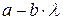 , для хрупких
, для хрупких  ,
,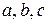 - постоянные коэффициенты, определяемые экспериментально для материалов.
- постоянные коэффициенты, определяемые экспериментально для материалов.
 от
от 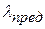 до
до 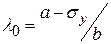 , т.е. для стержней средней гибкости.
, т.е. для стержней средней гибкости.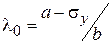 - вторая предельная гибкость.
- вторая предельная гибкость.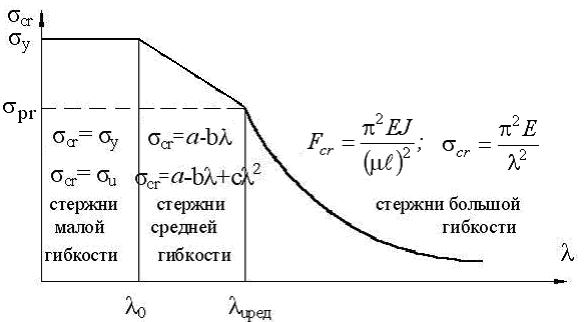
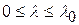 критическое напряжение равно пределу текучести
критическое напряжение равно пределу текучести  для хрупких материалов. Поэтому стержни малой гибкости рассчитываются не на устойчивость, а на прочность при сжатии.
для хрупких материалов. Поэтому стержни малой гибкости рассчитываются не на устойчивость, а на прочность при сжатии.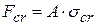 .
. . Величина
. Величина  , показывающая во сколько раз действующая сжимающая сила меньше критической, называется коэффициентом запаса устойчивости. Коэффициент запаса устойчивости принимается:
, показывающая во сколько раз действующая сжимающая сила меньше критической, называется коэффициентом запаса устойчивости. Коэффициент запаса устойчивости принимается:  - для стоек из сталей;
- для стоек из сталей;  - для стоек из древесины;
- для стоек из древесины; 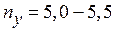 - для стоек из чугуна.
- для стоек из чугуна. Сжимающее напряжение при расчетах на устойчивость не должно превышать величины допускаемого напряжения
Сжимающее напряжение при расчетах на устойчивость не должно превышать величины допускаемого напряжения  при расчетах на устойчивость
при расчетах на устойчивость 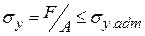 .
. ,
,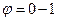 - коэффициент снижения основного допускаемого напряжения на сжатие.
- коэффициент снижения основного допускаемого напряжения на сжатие. .
. .
.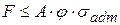 .
. ,
,  или
или 


