Расчётно-проектировочная работа № 6
«Расчёты на устойчивость продольно сжатых стержней» Пример 22. Для стойки из четырех уголков № 7, 5/5, 0× 0, 5 и четырех пластин размерами 20х1, 0 см, жёстко защемлённой нижним концом, из расчёта на устойчивость определить допускаемую сжимающую нагрузку и коэффициент запаса устойчивости Материал конструкционная сталь марки Ст.3, модуль номаль
Ход решения. 1. Определяем геометрическую гибкость стойки
где n = 0, 5 – число полуволн синусоиды изогнутой оси стойки, потерявшей устойчивость;
2. Определяем предельную гибкость для Ст3
3. Определяем критическую силу и критическое напряжение. При геометрической гибкости стойки
4. Определяем коэффициент снижения основного допускаемого напряжения на сжатие для Ст.3 при
5. Из условия устойчивости 6. Определяем коэффициент запаса устойчивости 1712, 8/755, 3 =2, 26, что в пределах допускаемой величины Примечания: 1. Если геометрическая гибкость будет больше табличной величины, то расчётную длину стойки в дальнейших расчётах уменьшить так, чтобы 2. Если геометрическая гибкость Если
Пример 23. Для стойки длиной
Ход решения
В первом приближении задаёмся
3. Для полученных размеров определяем геометрическую гибкость стержня где
4. Определяем коэффициент снижения основного допускаемого напряжения на сжатие для стойки из Ст.3 при
Коэффициент заданный и действительный тождественно не равны. 5. Во втором приближении задаётся Коэффициент снижения основного допускаемого напряжения для стойки из Ст.3 при
Коэффициент заданный и действительный тождественно не равны. 6. В третьем приближении задаёмся Тогда Коэффициент снижения основного допускаемого напряжения
Коэффициенты заданный и действительный практически равны. Для проверки правильности расчётов из условия устойчивости определяем допускаемую сжимающую нагрузку.
Вопросы и ответы для самоконтроля
1. Что называется устойчивостью? Способность сжатого стержня сохранять приданную ему при изготовлении первоначальную форму устойчивого равновесия называется устойчивостью. 2. Что называется потерей устойчивости? Потеря первоначальной формы устойчивого равновесия под действием продольной сжимающей силы называется потерей устойчивости. 3. Какая потеря устойчивости называется местной? Потеря устойчивости одним из элементов конструкции называется местной потерей устойчивости. 4. Какая потеря устойчивости называется общей? Потеря устойчивости несколькими или всеми элементами конструкции называется общей потерей устойчивости. 5. Какая сила называется критической? Минимальное значение продольной сжимающей силы, при котором происходит потеря первоначальной формы устойчивого равновесия сжатого стержня, называется критической силой. 6. Формула Л. Эйлера для определения критической силы.
6. Формула Л. Эйлера для определения критического напряжения.
нормальной упругости материала и обратно пропорционально квадрату геометрической гибкости стержня. 8. При каких напряжениях справедливы формулы Л. Эйлера для определения критических силы и напряжения? Формулы Л. Эйлера для определения критических силы и напряжения справедливы при напряжениях от 0 до предела пропорциональности 9. Формулы Ф.С. Ясинского для определения критических напряжений. Для пластических материалов 10. При каких напряжениях справедливы формулы Ф.С. Ясинского? Формулы Ф.С. Ясинского справедливы при критических напряжениях от предела пропорциональности 11. Что показывает коэффициент приведения длины стержня.
12. Что характеризует геометрическая гибкость стержня?
13. Какая гибкость называется первой предельной гибкостью?
14. Какая гибкость называется второй предельной гибкостью?
15. Какие стержни называются стержнями малой гибкости? Стержни у которых геометрическая гибкость 16. Какие стержни называются стержнями средней гибкости? Стержни у которых геометрическая гибкость 17. Какие стержни называются стержнями большой гибкости? Стержни у которых геометрическая гибкость 18. Формулы для определения коэффициента запаса устойчивости
19. Что показывает коэффициент запаса устойчивости? Коэффициент запаса устойчивости показывает во сколько раз значения сжимающих силы и напряжения меньше их критических значений. 20. Что показывает коэффициент снижения основного допускаемого на- пряжения? Коэффициент снижения основного допускаемого напряжения показывает какую часть составляет допускаемое напряжение на устойчивость от основного допускаемого напряжения на сжатие. 21. Как записывается условие устойчивости?
22. Решение задач по условию устойчивости. Проектировочная задача определения размеров сечения Проверочная задача определения допускаемой величины продольной сжимающей силы Проверочная задача проверки устойчивости и определения коэффициента запаса устойчивости
|

 ной упругости
ной упругости  , допускаемое напряжение на сжатие
, допускаемое напряжение на сжатие  , предел пропорциональности
, предел пропорциональности  . Длина стойки
. Длина стойки  . Концы стойки имеют одинаковый способ их закрепления в обоих главных плоскостях сечения, в соответствии с рисунком 7.4
. Концы стойки имеют одинаковый способ их закрепления в обоих главных плоскостях сечения, в соответствии с рисунком 7.4 ,
, - коэффициент приведения длины стойки, жёстко защемлённой одним концом;
- коэффициент приведения длины стойки, жёстко защемлённой одним концом; - минимальный радиус инерции сечения в плоскости с минимальной жесткостью стойки при изгибе, в которой происходит потеря устойчивости. Определение геометрических характеристик сечения рассмотрено в примере 2
- минимальный радиус инерции сечения в плоскости с минимальной жесткостью стойки при изгибе, в которой происходит потеря устойчивости. Определение геометрических характеристик сечения рассмотрено в примере 2
 ,
, для их расчёта принимаются формулы Л.Эйлера
для их расчёта принимаются формулы Л.Эйлера МПа
МПа кН
кН . По таблице коэффициента
. По таблице коэффициента  находим
находим
 Действительное значение
Действительное значение 





 определяем допускаемую нагрузку
определяем допускаемую нагрузку  кН
кН

 .
. , то критическое напряжение определяется по формуле Ясинского
, то критическое напряжение определяется по формуле Ясинского  , а
, а  , где а = 311 МПа, b = 11, 4 МПа – коэффициенты для Ст 3.
, где а = 311 МПа, b = 11, 4 МПа – коэффициенты для Ст 3. , то
, то  МПа,
МПа,  м, нагруженной сжимающей силой F 1 = 200 кН, из расчёта на устойчивость определить размеры прямоугольного поперечного сечения при h =2 b. Материал конструкционная сталь марки Ст3, основное допускаемое напряжение на сжатие
м, нагруженной сжимающей силой F 1 = 200 кН, из расчёта на устойчивость определить размеры прямоугольного поперечного сечения при h =2 b. Материал конструкционная сталь марки Ст3, основное допускаемое напряжение на сжатие  МПа. Способ закрепления концов стойки в обоих главных плоскостях считать одинаковым, в соответствии с рисунком 7.5.
МПа. Способ закрепления концов стойки в обоих главных плоскостях считать одинаковым, в соответствии с рисунком 7.5.
 или
или  Так как в условии устойчивости имеется два неизвестных, то задача решается методом последовательного приближения, при котором задаются одним из неизвестных. В данном варианте
Так как в условии устойчивости имеется два неизвестных, то задача решается методом последовательного приближения, при котором задаются одним из неизвестных. В данном варианте 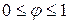 . Поэтому выгодно задаваться его величиной.
. Поэтому выгодно задаваться его величиной.
 . Тогда из условия устойчивости в первом приближении
. Тогда из условия устойчивости в первом приближении .
. м.
м.
 - коэффициент приведения длины стойки с шарнирно подвижной верхней и жестко защемленной нижней опорами;
- коэффициент приведения длины стойки с шарнирно подвижной верхней и жестко защемленной нижней опорами; - минимальный радиус инерции сечения.
- минимальный радиус инерции сечения. . По таблице находим
. По таблице находим
 Действительное значение
Действительное значение 


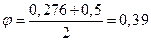 Тогда
Тогда  м,
м,  м.
м. 
 .
.
 Действительное значение
Действительное значение 


 м,
м,  м,
м, 
 Действительное значение
Действительное значение 


 кН, что больше заданной силы на
кН, что больше заданной силы на  . Это меньше точности расчётов ±5%.
. Это меньше точности расчётов ±5%. . Критическая сила прямо пропорциональна изгибной жесткости и обратно пропорциональна квадрату приведенной длинны стержня.
. Критическая сила прямо пропорциональна изгибной жесткости и обратно пропорциональна квадрату приведенной длинны стержня. . Критическое напряжение прямо пропорционально модулю
. Критическое напряжение прямо пропорционально модулю .
. для хрупких
для хрупких 
 до предела текучести
до предела текучести  для пластичных материалов и до предела прочности
для пластичных материалов и до предела прочности  для хрупких материалов.
для хрупких материалов. . Коэффициент проведения длины стержня, показывает во сколько раз необходимо изменить длину шарнирно закрепленного по концам стержня, чтобы критическая сила для него была равна критической силе для стержня при заданных способах его закрепления.
. Коэффициент проведения длины стержня, показывает во сколько раз необходимо изменить длину шарнирно закрепленного по концам стержня, чтобы критическая сила для него была равна критической силе для стержня при заданных способах его закрепления. . Геометрическая гибкость стержня характеризует способность стержня к потере устойчивости в зависимости от соотношения его продольных и поперечных размеров и способа закрепления концов.
. Геометрическая гибкость стержня характеризует способность стержня к потере устойчивости в зависимости от соотношения его продольных и поперечных размеров и способа закрепления концов. . Геометрическая гибкость стержня, при которой
. Геометрическая гибкость стержня, при которой 
 . Геометрическая гибкость стержня, при которой
. Геометрическая гибкость стержня, при которой 
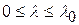
 .
.

 . Сжимающие напряжения прямо пропорциональное продольной сжимающей силе и обратно пропорциональное площади поперечного сечения стержня не должно превышать допускаемого напряжения на устойчивость.
. Сжимающие напряжения прямо пропорциональное продольной сжимающей силе и обратно пропорциональное площади поперечного сечения стержня не должно превышать допускаемого напряжения на устойчивость. .
.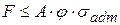 .
. ,
,  или
или  .
.


