Критерий Райта. Результат измерения xi (xmax или xmin)не принадлежит заданному распределению (т
Результат измерения xi (xmax или xmin)не принадлежит заданному распределению (т. е. отягощен грубой погрешностью или промахом) с заданной вероятностью Р, если
где tp — доверительный коэффициент, или, другими словами, если xi выходит за границы интервала Для нормального распределения обычно выбирают Р= 0, 9973, для которого tp= 3, поэтому в этом случае критерий известен под названием " правило 3-х сигм". Вероятность отклонения " нормального" результата наблюдения за указанные границы в этом случае равна малой величине 1- Аналогичным образом можно сформулировать данный критерий и для других распределений. Так, для распределения Лапласа значение tр для вероятности 0, 9973 равно 4, 18. Для распределений, обладающих, в отличие от нормального, границами, следует выбирать Р= 1. В этом случае вероятность появления результатов наблюдения за границами распределения равна нулю. Значения tp для разных распределений указаны в табл. 2.1. Таблица 2.1 Значения tp для различных распределений
Недостаток критерия — он справедлив для выборок с количеством наблюдений n > 20..30, для которых можно считать, что 2.1.1.2 Критерий: Смирнова При n < 20..30 для обнаружения грубых погрешностей и промахов пользуются критерием Смирнова, для которого выражение (2.1) принимает вид
где b - случайная величина, зависящая не только от вероятности Р, но и от числа наблюдений п. Зависимость b от п для разных Р длянормального закона распределения результатов наблюдений имеет вид, указанный на рис. 2.1. В табл. Б.1 приложения приведены зависимости b (n) для разных законов распределения.
Рисунок 2.1 - Зависимость b (n) в критерии Смирнова для нормального закона распределения 2.1.2 Критерии согласия По виду кумулятивной кривой и гистограммы, а также по полученным экспериментально оценкам эксцесса и асимметрии, высказывают гипотезу о виде распределения результатов наблюдения. Правдоподобие гипотезы о соответствии распределения результатов наблюдения выбранному закону проверяют с помощью так называемых критериев согласия. Таких критериев существует множество. Рассмотрим некоторые из них, нашедшие наибольшее применение на практике. 2.1.2.1 Критерий Колмогорова В этом критерии в качестве меры расхождения кумулятивной кривой
Колмогоров доказал, что какова бы ни была функция распределения
стремится к пределу
Зависимость Схема применения критерия Колмогорова заключается в следующем: 1) строится кумулятивная кривая 2) определяется величина 3) по таблице Б.2 находится вероятность
Рисунок 2.2 - Зависимость Критерий Колмогорова очень прост и поэтому его охотно применяют на практике. Следует, однако, заметить, что этот критерий можно применять только в случае, когда гипотетическое распределение 2.1.2.2 Критерий Пирсона В качестве меры расхождения гистограммы с теоретическим дифференциальным законом распределения вероятностей в критерии Пирсона принимается величина
где т — число результатов наблюдений, попавших на j -й интервал гистограммы;
Значение
где п — общее число наблюдений;
Величина c распределена по закону Пирсона (рис.2.3). Распределение зависит от параметра k, называемого числом " степеней свободы". Число степеней свободы равно числу интервалов гистограммы L, минус число независимых условий, наложенных на эмпирическое распределение. Для симметричных законов распределения такими условиями являются: 1) условие нормировки 2) требование равенства математического ожидания гипотетического распределения среднему арифметическому экспериментального распределения
3) требование равенства дисперсии гипотетического распределения оценке дисперсии экспериментального распределения
Рисунок 2.3 - Интегральная функция распределения Пирсона Поэтому k=L-3. Для распределения Пирсона составлены соответствующие таблицы (см. табл. Б. З). Пользуясь этими таблицами можно найти для каждого На практике вероятностью При проверке закона распределения по критерию Пирсона хорошие результаты получаются только если п> 40..50. 2.1.2.3 Составной критерий Составной критерий применяется для п, лежащего в диапазоне от 10..15 до 40..50, обычно, для проверки принадлежности экспериментального распределения нормальному. Критерий состоит из двух частей. 1. В первой части критерия для ряда наблюдений рассчитывается величина
и проверяется выполнение условий 2. Во второй части критерия определяют количество т результатов наблюдений, которые выходят за границы интервала
где
Для законов распределения, отличных от нормального, значения коэффициента d берется из табл. Б.4, а значения доверительного коэффициента
Рисунок 2.4 - Зависимость d от п в составном критерии 2.1.3 Интервальные оценки распределения результатов наблюдений и измерения Доверительным интервалом называется интервал, границы которого симметричны относительно математического ожидания, а вероятность попадания в который результата измерений равна доверительной. На рис. 2.5 видно, что ширина доверительного интервала 2 e зависит от доверительной вероятности Если закон распределения неизвестен, то для оценки доверительного интервала следует воспользоваться неравенством Чебышева. Для вывода неравенства оценим вероятность того, что измеряемая величина не попадает в доверительный интервал
По определению дисперсия X равна квадрату среднеквадратического отклонения и выражается формулой
В формуле (2.6) положим подынтегральное выражение равным нулю на интервале
Так как по начальному условию
Правая часть неравенства (2.8) совпадает с правой частью выражения (2.5). Учитывая это, можно записать
откуда В предельном случае
где
Рисунок 2.5 - Доверительная вероятность и доверительный интервал Значения
откуда, в предельном случае
Значения Таблица 2.2 Зависимости доверительного коэффициента
Для известных законов распределения значения доверительного коэффициента можно найти из выражения
подставляя вместо
Равновероятное распределение (рис. А1, а). Плотность распределения
Интегральная функция распределения
Числовые характеристики распределения — математическое ожидание Доверительная вероятность
Отсюда Треугольное распределение (Симпсона) (рис. А.1, б). Плотность распределения
Интегральная функция распределения
Числовые характеристики
Доверительная вероятность
Отсюда
Нормальный закон (Гауса) (рис. А.1, в). Плотность распределения
Интегральная функция распределения
Доверительная вероятность
Вводим замену переменного
т. е. где Отсюда получаем Значение функции Двойное экспоненциальное распределение (Лапласа) (рис. АЛ, г). Плотность распределения
Интегральная функция распределения
Среднеквадратическое отклонение
Доверительная вероятность
Отсюда
Распределение по закону арксинуса (рис. А1, д). Плотность распределения
Интегральная функция распределения
Доверительная вероятность
Отсюда
Зависимости числовых значений доверительных коэффициентов
2.1.4 Минимизация случайной погрешности Уменьшить случайную погрешность можно, определяя оценку математического ожидания многократных наблюдений измеряемой величины X. В этом случае за результат измерения, как правило, принимается среднее арифметическое результатов наблюдений
Поскольку Дисперсия среднего арифметического результатов наблюдений Поэтому, принимая за результат измерения Границы погрешности среднего арифметического будут, очевидно, определяться выражением
Для определения границ погрешности среднего арифметического необходимо знать его закон распределения. Центральная предельная теорема теории вероятности гласит: если имеется п независимых случайных величин xi распределенных по одному и тому же закону с математическим ожиданием МX и дисперсией DX, то при неограниченном увеличении п закон распределения суммы Если п < 20..30, то распределение х уже нельзя считать нормальным. Как же определить Доверительная вероятность для Деля обе части неравенства на
получаем
Обозначим
где Закон распределения Т зависит от закона распределения xi, и числа наблюдений п. Из теории вероятности известно, что если величина xi распределена по нормальному закону, то величина Т распределена по так называемому закону Стьюдента с k= (n- 1) степенью свободы. Плотность распределения Стьюдента имеет вид (рис. 2.6)
где С ростом п распределение Стьюдента приближается к нормальному и при n > 20..30 уже неотличимо от него (рис. 2.6). Таким образом, если известно, что результаты отдельных наблюдений распределены по нормальному закону, то при числе наблюдений n =2..20 при определении границ случайной погрешности доверительный коэффициент
где
На рис. 2.8 приведен порядок определения границ случайной погрешности результата измерения.
2.2 Пример выполнения контрольного задания 2.2.1 Задание Определите границы случайной погрешности результатов многократных измерений, приведенных в примере выполнения контрольного задания в разделе 1 (пп. 1.2.1), для доверительной вероятности 2.2.2 Выполнение задания По виду гистограммы и кумулятивной кривой заданных результатов наблюдений, а также по полученным точечным оценкам асимметрии и эксцесса, высказываем гипотезу о том, что результат наблюдения распределен по нормальному закону. 1. Определение грубых погрешностей и промахов по критерию Райта. Результат измерения xi (xmax или xmin)не принадлежит нормальному распределению с заданной вероятностью Р, если
т. е. если xi, - выходит за границы интервала 2. Определение грубых погрешностей и промахов по критерию Смирнова. По°критерию Смирнова результат измерения xi не принадлежит заданному распределению с заданной вероятностью Р, если
где b - случайная величина, зависимая от Р и числа наблюдений n. Для числа измерений n= 40 и уровня значимости
3. Проверка по критерию Пирсона Для полученных ранее значений средин интервалов гистограммы, рассчитываем значения плотности вероятности теоретического распределения, воспользовавшись формулой (2.20)
и занесем их в таблицу (2.3). Вычисляем частоты
Вычисленные значения Таблица 2.3 Результаты расчета
Рассчитаем для каждого интервала j значение Определим суммарное значение По таблице Б. З для заданной вероятности Р=0, 95 и числа степеней свободы k= 7–3=4 находим значение Так как
|

 , (2.1)
, (2.1) .
.


 и
и  .
. (2.2)
(2.2)
 и теоретической (действительной) интегральной функцией распределения
и теоретической (действительной) интегральной функцией распределения  взято максимальное значение модуля разности
взято максимальное значение модуля разности .
.
 .
. изображена на рис. 2.2 и приведена в табл. Б.2.
изображена на рис. 2.2 и приведена в табл. Б.2. , где п — число наблюдений;
, где п — число наблюдений;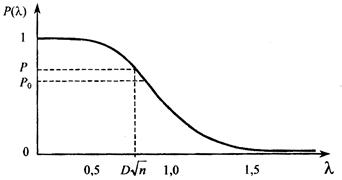
 в критерии Колмогорова
в критерии Колмогорова
 , (2.3)
, (2.3) - действительное число результатов наблюдений, которые попали бы на j - й интервал, при полном соответствии эмпирического закона распределения гипотетическому.
- действительное число результатов наблюдений, которые попали бы на j - й интервал, при полном соответствии эмпирического закона распределения гипотетическому. ,
, - значение гипотетической функции распределения в точке, соответствующей средине j -го интервала гистограммы, j= 1, 2,.., L;
- значение гипотетической функции распределения в точке, соответствующей средине j -го интервала гистограммы, j= 1, 2,.., L; - ширина интервала гистограммы.
- ширина интервала гистограммы. ;
;


 и числа степеней свободы вероятность
и числа степеней свободы вероятность  того, что величина, распределенная по закону
того, что величина, распределенная по закону  , превзойдет это значение.
, превзойдет это значение. . Если
. Если  то гипотеза о виде закона распределения подтверждается, если
то гипотеза о виде закона распределения подтверждается, если  то отклоняется.
то отклоняется. (2.4)
(2.4) , где
, где  и
и  зависят от вероятности Р (рис. 2.4), с которой принимается решение и находятся по табл. Б.4. Если это условие выполняется, переходят ко второй части критерия.
зависят от вероятности Р (рис. 2.4), с которой принимается решение и находятся по табл. Б.4. Если это условие выполняется, переходят ко второй части критерия. ,
,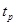 - доверительный коэффициент (для нормального распределения
- доверительный коэффициент (для нормального распределения 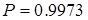 и
и 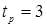 );
); - оценка среднеквадратического отклонения. При числе наблюдений n < 20, т не должно быть больше 1, а при n > 20, т < 2. Если и это условие выполняется, то гипотеза о нормальности распределения подтверждается. При невыполнении одного из условий гипотеза отклоняется.
- оценка среднеквадратического отклонения. При числе наблюдений n < 20, т не должно быть больше 1, а при n > 20, т < 2. Если и это условие выполняется, то гипотеза о нормальности распределения подтверждается. При невыполнении одного из условий гипотеза отклоняется. для проверки по второй части критерия — из табл. 2.1.
для проверки по второй части критерия — из табл. 2.1.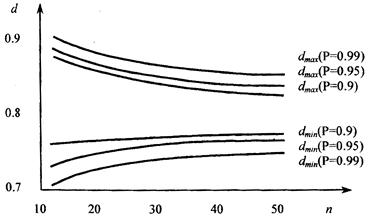
 , вида распределения и его среднеквадратического отклонения, которое характеризует степень рассеяния результатов измерений вокруг математического ожидания
, вида распределения и его среднеквадратического отклонения, которое характеризует степень рассеяния результатов измерений вокруг математического ожидания  .
. :
: . (2.5)
. (2.5) . (2.6)
. (2.6) (2.7)
(2.7) , то заменив в неравенстве (2.7)
, то заменив в неравенстве (2.7)  на e мы усиливаем это неравенство, получая
на e мы усиливаем это неравенство, получая . (2.8)
. (2.8) ,
, . (2.9)
. (2.9) ,
, - т. н. доверительный коэффициент, зависящий от доверительной вероятности. Зависимость
- т. н. доверительный коэффициент, зависящий от доверительной вероятности. Зависимость  , для неизвестного закона распределения, вытекающая из неравенства Чебышева, представлена в табл. 2.2.
, для неизвестного закона распределения, вытекающая из неравенства Чебышева, представлена в табл. 2.2.
 . Поэтому для симметричных законов распределения можно воспользоваться неравенством Кампа-Мейделя
. Поэтому для симметричных законов распределения можно воспользоваться неравенством Кампа-Мейделя , (2.10)
, (2.10) . (2.11)
. (2.11) для различных законов распределения
для различных законов распределения , (2.12)
, (2.12) соответствующее аналитическое выражения для интегральной функции распределения результатов или погрешностей измерения.
соответствующее аналитическое выражения для интегральной функции распределения результатов или погрешностей измерения. (2.13)
(2.13) (2.14)
(2.14) ; среднеквадратическое отклонение
; среднеквадратическое отклонение  .
. . (2.15)
. (2.15) ;
;  .
. (2.16)
(2.16) (2.17)
(2.17)
 (2.18)
(2.18)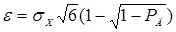 ;
;  (2.19)
(2.19) . (2.20)
. (2.20) . (2.21)
. (2.21) .
. , откуда
, откуда  и вместо
и вместо  в пределах интегрирования необходимо записать
в пределах интегрирования необходимо записать ,
, ,
, – функция Лапласа.
– функция Лапласа. .
. , обратной функции Лапласа, табулированы (табл. Б.6).
, обратной функции Лапласа, табулированы (табл. Б.6). . (2.23)
. (2.23) (2.24)
(2.24)
 .
. ;
;  . (2.25)
. (2.25) (2.26)
(2.26) (2.27)
(2.27) .
. ,
,  . (2.28)
. (2.28) для различных законов распределения приведены в табл. 2.2.
для различных законов распределения приведены в табл. 2.2. .
.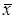 определяется по конечному числу наблюдений, то является случайной величиной.
определяется по конечному числу наблюдений, то является случайной величиной. в п раз меньше дисперсии однократного наблюдения
в п раз меньше дисперсии однократного наблюдения 
 (2.29)
(2.29) неограниченно приближается к нормальному. Считается, что при п> 20..30 центральная предельная теорема соблюдается, поэтому в этом случае значения доверительного коэффициента в выражении (2.29) берется из таблицы для нормального распределения.
неограниченно приближается к нормальному. Считается, что при п> 20..30 центральная предельная теорема соблюдается, поэтому в этом случае значения доверительного коэффициента в выражении (2.29) берется из таблицы для нормального распределения. равна
равна  .
. ,
,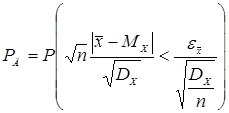 (2.30)
(2.30)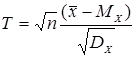 , тогда
, тогда ,
,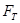 - интегральная функция распределения величины Т.
- интегральная функция распределения величины Т. ,
, ,
,  - гамма-функция.
- гамма-функция. приведена на рис. 2.7 и в табл. Б.5. При отсутствии таблиц с распределением Стьюдента, значение коэффициента
приведена на рис. 2.7 и в табл. Б.5. При отсутствии таблиц с распределением Стьюдента, значение коэффициента  для n =6..20 можно определить приближенно (с погрешностью до 20 %) по формуле
для n =6..20 можно определить приближенно (с погрешностью до 20 %) по формуле ,
, - доверительный коэффициент для нормального распределения.
- доверительный коэффициент для нормального распределения.
 для распределения Стьюдента
для распределения Стьюдента

 и уровня значимости критериев согласия
и уровня значимости критериев согласия  .
. где
где  их оценки
их оценки  и
и  , с учетом того, что для нормального закона распределения
, с учетом того, что для нормального закона распределения  (для вероятности
(для вероятности  и значение b по табл. Б.1 равно 3, 07. Тогда интервал
и значение b по табл. Б.1 равно 3, 07. Тогда интервал  будет равен (1, 693845; 8, 702655), т. е. все результаты измерения xi принадлежат нормальному распределению.
будет равен (1, 693845; 8, 702655), т. е. все результаты измерения xi принадлежат нормальному распределению. попаданий результатов наблюдений, подчиняющихся теоретическому распределению по формуле:
попаданий результатов наблюдений, подчиняющихся теоретическому распределению по формуле: .
. экспериментального распределения заносим в табл.2.3.
экспериментального распределения заносим в табл.2.3.
 и занесем их в табл. 2.3.
и занесем их в табл. 2.3. .
. .
. , то это свидетельствует о том, что гипотеза о нормальном распределении экспериментальных данных верна.
, то это свидетельствует о том, что гипотеза о нормальном распределении экспериментальных данных верна.


