Проверка по критерию Колмогорова
Полученные ранее значения кумулятивной кривой на границах интервалов xj занесем в табл. 2.4. Таблица 2.4 Результаты расчета
Для полученных ранее оценок математического ожидания
где Занесем полученные значения Найдем значения По табл. Б.2 определим соответствующую рассчитанному значению l вероятность 5. Проверка по составному критерию Для заданного в примере ряда наблюдений рассчитаем значение d по формуле:
Согласно табл. Б.4, для заданной вероятности Для проверки " хвостов" эмпирического распределения по второй части критерия определим половину доверительного интервала по формуле: 6. Определение границ случайной погрешности результатов наблюдения и измерения Границы случайной погрешности результатов наблюдения определим по формуле Границы случайной погрешности результата измерения (среднего арифметического) находим по формуле 2.3 Варианты контрольных заданий Определите границы случайной погрешности результатов многократных измерений, приведенных в разделе 1 (пп. 1.2.3), для заданных в табл.2.5 доверительной вероятности Таблица 2.5 Варианты заданий
3 ПОСТРОЕНИЕ И ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК КОМПОЗИЦИИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ПРИ СУММИРОВАНИИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ 3.1 Основные теоретические сведения Погрешность измерения, как правило, вызывается разнообразными одновременно действующими причинами и поэтому может состоять из большого числа т составляющих. Рассмотрим, как из этих составляющих
Каждую из составляющих
Известно, что каждая из составляющих включает в себя две компоненты — случайную
Таким образом, при формировании результирующей погрешности Случайные погрешности характеризуются своими границами
Значение доверительного коэффициента Таблица 3.1 Границы погрешности
Для
При неизвестном законе распределения
При
При Значения коэффициентов Таблица 3.2 Значения
Если неизвестные законы распределения заданы границами
Зависимость коэффициента
Рисунок 3.1 - Зависимость коэффициента Как видно из рис. 3.1, максимальное значение При известных законах распределения случайной погрешности, как уже было сказано выше, необходимо осуществить построение композиции законов распределения. Для нахождения композиции двух известных законов распределения
где Однако найти решение (3.10) в аналитическом виде можно далеко не всегда. Кроме того, на практике могут быть известны не законы распределения составляющих случайных погрешностей, а их гистограммы, получаемые в результате практических исследований
Здесь Расписывая это уравнение для разных значений q, получаем
Таким образом, результирующая гистограмма будет содержать Необходимым условием осуществления метода перебора является одинаковая ширина столбиков гистограмм. В этом случае методика определения гистограммы результирующего распределения сводится к следующим операциям. 1. Гистограммы эмпирических законов распределения, заданные в табличной форме, представляются в виде верхней строки (головки) и левого столбца (боковика) таблицы 3.3. 2. В клетках таблицы, находящихся на пересечении столбца 3. Производится суммирование всех произведений 4. Полученные суммы умножают на ширину столбика гистограммы и получают значение высот столбиков гистограммы композиции законов распределения, которые представляют в табличной форме аналогично первоначальным гистограммам. Нахождение композиции Если законы распределения заданы аналитически, то высоты столбиков гистограммы определяются по формуле
Таблица 3.3 Таблица для построения гистограммы композиции двух законов распределений
Для законов распределения, график которых составлен из отрезков линий (трапециидальный, треугольный, равномерный), высоты столбиков гистограммы Оценки математического ожидания и дисперсии результирующего закона распределения можно найти по формулам
Границы погрешности можно определить непосредственно из гистограммы, находя границы доверительного интервала, соответствующего заданной доверительной вероятности. Последняя соответствует площади под гистограммой, ограниченной перпендикулярами, возведенными из точек на оси абсцисс, соответствующих границам погрешности (рис. 3.2).
3.2 Пример выполнения контрольного задания 3.2.1 Задание Постройте композицию заданных в табл. 3.4 законов распределения суммы трех составляющих погрешности
и найдите оценки ее математического ожидания и дисперсии. Таблица 3.4 - Законы распределения составляющих погрешности
3.2.2 Выполнение задания 1. Построим гистограммы законов распределения (рис. 3.3), учитывая, что значения х соответствуют серединам столбиков гистограмм, а
Рисунок 3.3 - Гистограммы заданных законов распределения Таблица 3.5 Построение композиции первых двух законов распределения
2. Осуществляем композицию первых двух законов распределения, для чего представим их в виде верхней строки и левого столбца таблицы 3.5. Заполнение табл. 3.5 осуществляем аналогично табл. 3.3. 3. После заполнения таблицы 3.5 производится суммирование произведений Р1(х)-р2(х), имеющих одинаковые суммы аргументов xi+xj (лежащие на одной диагонали табл. 3.5). Перемножая полученные суммы на
Рисунок 3.4 - Гистограмма композиции двух первых законов распределения 4. Добавляем к полученному дискретному закону распределения третий закон распределения в виде левого столбца таблицы 3.6, и заполняя таблицу также, как и 3.5, получаем композицию трех законов распределения (табл. 3.7), гистограмма которой приведена на рис. 3.5. Таблица 3.6 Построение композиции трех законов распределения
Таблица 3.7 Композиция трех законов распределения
Рисунок 3.5 - Гистограмма композиции трех законов распределения 5. Из рис. 3.5 видно, что полученный закон распределения по форме близок к нормальному. Оценки математического ожидания 3.3 Контрольное задание Постройте композицию заданных в табл. 3.8 и 3.9 законов распределения суммы четырех составляющих погрешности X = Х1 + Х2 + Х3 + Х4 и найдите оценки математического ожидания и дисперсии получаемого распределения. Таблица 3.8 Варианты заданий
Таблица 3.9 Законы распределения
4 ОБРАБОТКА НЕСКОЛЬКИХ ГРУПП ПРЯМЫХ ИЗМЕРЕНИЙ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ 4.1 Основные теоретические сведения На практике одну и ту же величину могут измерять разными СИТ, в разное время или в разных условиях, получая несколько (больше одной) групп наблюдений. Для повышения точности естественно объединить эти результаты, т.е. выполнить совместную обработку этих групп. Однако к повышению точности объединение результатов приведет лишь при определенных условиях, а именно при статистической однородности групп наблюдений. Статистическая однородность групп наблюдений заключается в выполнении следующих условий: 1) наблюдения в группах распределены по одному и тому же закону; 2) средние арифметические групп различаются незначительно; 3) дисперсии групп различаются незначительно (т.е. результаты равнорассеяны или, как говорят, равноточны). Проверка соответствия распределения наблюдений в группах одному и тому же закону осуществляется с помощью критериев согласия (см. раздел 2). Дальнейшая проверка статистической однородности осуществляется с помощью аппарата математической статистики, называемого дисперсионным анализом. Проверка однородности групп по математическому ожиданию при числе групп L > 3 осуществляется с помощью методов Аббе или Фишера. Метод Аббе заключается в следующем. Определяют средние арифметические значения групп наблюдений в порядке их получения:
где nj - число наблюдений в j -й группе. Определяют дисперсию отклонения соседних групп:
Отношение v = D2 / D1 должно быть меньше некоторого vKp. Критическое значение vKp в зависимости от уровня значимости q и числа групп L табулировано (см. график рис. 4.1).
Рисунок 4.1 - Распределение Аббе Метод Фишера состоит в сравнении оценок межгрупповой дисперсии dl и средней дисперсии групп D
где Обе оценки дисперсии имеют распределение Рассеивание средних арифметических считают допустимым, если F= DL/D при выбранной вероятности а лежит в пределах от FH до Fв P{FH где Fв определяется по таблице распределения Фишера (см. таблицу B.7), aFw=l/Fe. Для F=2 можно воспользоваться более простым критерием, алгоритм осуществления которого приведен на рис. 4.2. Он состоит в следующем. 1. Определяются средние арифметические для каждой группы наблюдений по формулам
где x1i, x2-результаты наблюдений из 1-й и 2-й групп; 2. Вычисляется модуль разности, полученных средних арифметических:
3. Находятся оценки дисперсии результатов наблюдений в каждой из групп по формулам
4. Определяется суммарная оценка дисперсии результатов измерения этих групп:
5. По заданной доверительной вероятности Р д, считая закон распределения модуля разности средних арифметических наблюдений групп, нормальным (для п1+п2 > 30), определяются по табл. 2.2 значение коэффициента tp, после чего производится сравнение G и tp Если G < tp Для проверки равнорассеянности (равноточности) измерений в группах следует воспользоваться следующим алгоритмом (рис. 4.2). 1. По вычисленным значениям
2. Выбирается доверительная вероятность и по табл. Б.7 распределения Фишера (а именно по такому закону оказывается распределенной величина 3. Производится сравнение В зависимости от полученных результатов производится дальнейшая обработка групп измерений. 4.1.1 Измерения равноточные Оценку математического ожидания результатов наблюдений (результат измерения) для объединенных групп определяют по формуле
Рисунок 4.2 - Алгоритм обработки двух групп наблюдений
Оценка дисперсии результата измерения, очевидно, описывается выражением
Для преобразования этого выражения величину
Так как с учетом выражения (4.6)
то эту сумму можно записать следующим образом
Поскольку то окончательное выражение для оценки дисперсии результата измерения будет иметь вид
После получения оценки дисперсии вычисляются границы случайной погрешности по формуле (2.29)
в которой 4.1.2 Измерения неравноточные При неравнорассеянных результатах измерения в группах их объединение осуществляется таким образом, чтобы получить наиболее эффективную оценку математического ожиданиях. Эту оценку будем искать, используя принцип максимального правдоподобия (пп.1.1.4). Если средние арифметические в группах Xj можно считать распределенными по нормальному закону, то функцию правдоподобия можно представить в виде
Логарифмическая функция правдоподобия
Нам нужно найти эффективную оценку
Отсюда
Это так называемое средневзвешенное, которое принимается за оценку математического ожидания объединенных групп. Для равных дисперсий из выражения (4.10) получаем выражение (4.5). Оценка дисперсии
После получения оценки дисперсии вычисляют границы случайной погрешности по формуле (2.29)
в которой 4.2 Пример выполнения контрольного
|

 и СКО
и СКО  рассчитаем по формуле интегральной функции нормального распределения значения
рассчитаем по формуле интегральной функции нормального распределения значения  в точках xj
в точках xj
 - значения функции Лапласа (табл. Б.6).
- значения функции Лапласа (табл. Б.6).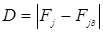 и занесем их в табл. 2.4. Определим максимальное значение
и занесем их в табл. 2.4. Определим максимальное значение 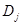 из числа рассчитанных:
из числа рассчитанных: 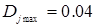 . Найдем значение
. Найдем значение  .
. . В святи с тем, что
. В святи с тем, что  , то гипотезу о нормальном законе распределения можно считать верной.
, то гипотезу о нормальном законе распределения можно считать верной. .
.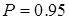 , значение d должно находиться в интервале от 0, 747 до 0, 854, т. е. заданные результаты наблюдений удовлетворяют первой части составного критерия.
, значение d должно находиться в интервале от 0, 747 до 0, 854, т. е. заданные результаты наблюдений удовлетворяют первой части составного критерия. . Для нормального распределения
. Для нормального распределения  (из табл. 2.2), поэтому
(из табл. 2.2), поэтому 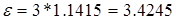 , а границы доверительного интервала будут равны
, а границы доверительного интервала будут равны  ;
;  . Ни один результат наблюдений не выходит за указанные границы, поэтому все они удовлетворяют второй части критерия. Таким образом, определили, что результаты наблюдений подчиняются нормальному закону распределения.
. Ни один результат наблюдений не выходит за указанные границы, поэтому все они удовлетворяют второй части критерия. Таким образом, определили, что результаты наблюдений подчиняются нормальному закону распределения.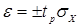 . Из табл.2.2 для вероятности
. Из табл.2.2 для вероятности  для нормального распределения находим
для нормального распределения находим  . Поэтому
. Поэтому  .
. , где коэффициент
, где коэффициент 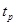 берется из табл. 2.2 в любом случае для нормального распределения (при п> 20–30). Поэтому для заданной вероятности
берется из табл. 2.2 в любом случае для нормального распределения (при п> 20–30). Поэтому для заданной вероятности  ;
;  .
. и уровня значимости критериев согласия a.
и уровня значимости критериев согласия a. (считаемых независимыми) формируется результирующая погрешность
(считаемых независимыми) формируется результирующая погрешность
 результирующей погрешности
результирующей погрешности  является композицией законов распределения
является композицией законов распределения  составляющих
составляющих 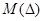 и дисперсия
и дисперсия  распределения результирующей погрешности является суммой соответственно математических ожиданий и дисперсий составляющих
распределения результирующей погрешности является суммой соответственно математических ожиданий и дисперсий составляющих 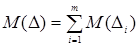 (3.1)
(3.1) (3.2)
(3.2) и систематическую
и систематическую  . Поскольку случайная погрешность — величина центрированная (т. е. для нее справедливо
. Поскольку случайная погрешность — величина центрированная (т. е. для нее справедливо  ), а систематическая компонента является постоянной величиной с нулевой дисперсией
), а систематическая компонента является постоянной величиной с нулевой дисперсией 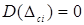 , то
, то  , и
, и  , и поэтому
, и поэтому (3.3)
(3.3) . (3.4)
. (3.4) , поэтому такой подход к их суммированию применен быть не может. Действительно, как следует из (3.4), границы e случайной компоненты результирующей погрешности будут равны
, поэтому такой подход к их суммированию применен быть не может. Действительно, как следует из (3.4), границы e случайной компоненты результирующей погрешности будут равны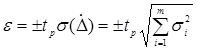 . (3.5)
. (3.5) в выражении (3.5) зависит от доверительной вероятности
в выражении (3.5) зависит от доверительной вероятности  и вида суммарного распределения случайных составляющих погрешности
и вида суммарного распределения случайных составляющих погрешности  и доверительный коэффициент
и доверительный коэффициент 
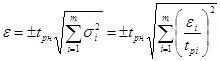


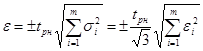
 , независимо от законов распределения
, независимо от законов распределения  (см. табл. 3.1). Композиция нормальных законов распределения для любого m также является нормальным распределением, поэтому
(см. табл. 3.1). Композиция нормальных законов распределения для любого m также является нормальным распределением, поэтому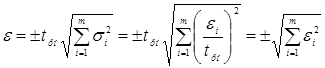 . (3.6)
. (3.6) , равновероятно, поэтому закон распределения всех
, равновероятно, поэтому закон распределения всех  (для
(для  ), поэтому для
), поэтому для 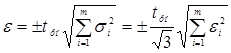 . (3.7)
. (3.7) доверительный коэффициент
доверительный коэффициент  ,)
,) . (3.8)
. (3.8) композиция дает трапециидальное (а при равенстве дисперсий — треугольное) распределение (для
композиция дает трапециидальное (а при равенстве дисперсий — треугольное) распределение (для  ); при
); при  - параболическое распределение (для
- параболическое распределение (для  ) и т. д.
) и т. д. то при
то при  . (3.9)
. (3.9) от числа слагаемых т и соотношения между погрешностями
от числа слагаемых т и соотношения между погрешностями  , для
, для  , приведена на рис. 3.1.
, приведена на рис. 3.1.
 от числа слагаемых т и соотношения между погрешностями с
от числа слагаемых т и соотношения между погрешностями с и равно
и равно  , где
, где  можно воспользоваться уравнением свертки
можно воспользоваться уравнением свертки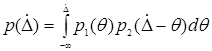 , (3.10)
, (3.10)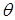 - переменная интегрирования, имеющая размерность погрешности.
- переменная интегрирования, имеющая размерность погрешности.
 (3.11)
(3.11) - ширина столбиков гистограмм;
- ширина столбиков гистограмм;  - их высота;
- их высота; 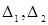 - абсциссы середин первых столбиков гистограмм;
- абсциссы середин первых столбиков гистограмм; 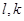 - число столбиков гистограмм
- число столбиков гистограмм  .
. ;
;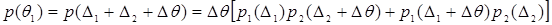 ;
;


 столбиков.
столбиков.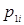 , и строки
, и строки  записывается произведение высот столбиков
записывается произведение высот столбиков  и сумма их абсцисс
и сумма их абсцисс  .
.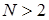 законов распределения производится по указанной методике последовательно
законов распределения производится по указанной методике последовательно  раз.
раз.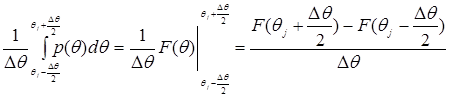 (3.12)
(3.12)


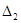

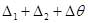
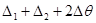


 можно определять как значения дифференциальной функции распределения
можно определять как значения дифференциальной функции распределения  соответствующих серединам интервалов гистограммы. Однако, для законов распределения с нелинейным изменением плотности вероятности на интервале
соответствующих серединам интервалов гистограммы. Однако, для законов распределения с нелинейным изменением плотности вероятности на интервале  ; (3.13)
; (3.13) (для случайных погрешностей);
(для случайных погрешностей); . (3.14)
. (3.14)

 - их высотам. Из рис. 3.3 видно, что первое распределение можно отнести к распределениям вида арксинус, второе — к треугольному, а третье — к равномерному. Ширина интервалов для всех гистограмм
- их высотам. Из рис. 3.3 видно, что первое распределение можно отнести к распределениям вида арксинус, второе — к треугольному, а третье — к равномерному. Ширина интервалов для всех гистограмм  равна 0, 1.
равна 0, 1.
 получаем композицию первых двух законов распределения (верхняя строка в табл. 3.6). Гистограмма полученного распределения изображена на рис. 3.4.
получаем композицию первых двух законов распределения (верхняя строка в табл. 3.6). Гистограмма полученного распределения изображена на рис. 3.4.

 и дисперсии
и дисперсии  для этого распределения рассчитываем по формулам (3.13) и (3.14):
для этого распределения рассчитываем по формулам (3.13) и (3.14): 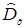 =0, 047.
=0, 047.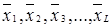 . Определяют дисперсию средних арифметических групп
. Определяют дисперсию средних арифметических групп
 ;
;  ;
; 


 ;
; 
 с числом степеней свободы соответственно k1=L-1; k 2 = N - L.
с числом степеней свободы соответственно k1=L-1; k 2 = N - L.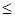 F
F  Fe } =
Fe } =  ,
,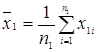 ;
; 
 (4.1)
(4.1) . (4.2)
. (4.2)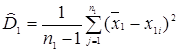 ,
,  . (4.3)
. (4.3) (4.4)
(4.4) .
.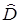 1и
1и  или
или  , так, чтобы
, так, чтобы 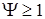 .
. ) находится значение параметра
) находится значение параметра  для заданных n1 и п2.
для заданных n1 и п2.
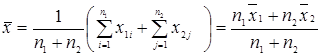 . (4.5)
. (4.5) .
.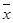 представим как
представим как .
. .
. .
. ,
, . (4.7)
. (4.7) ,
, . (4.8)
. (4.8) . (4.9)
. (4.9)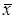 , поэтому приравниваем нулю производную L по
, поэтому приравниваем нулю производную L по 
 (4.10)
(4.10) . (4.11)
. (4.11)


