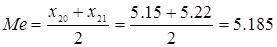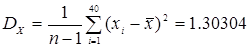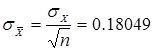Выполнение задания
1. Расположим результаты наблюдений xi в порядке возрастания и занесем их в табл. 1.4. 2. Взяв из таблицы минимальное и максимальное значения xi, определим диапазон
3. В соответствии с рекомендациями табл. 1.1 разобьем этот диапазон на L =7 интервалов шириной
Определим границы интервалов Отметим границы интервалов горизонтальными чертами в табл. 1.4. 4. Посчитаем количество mj результатов наблюдений, попавших в каждый интервал j и занесем в табл.1.4. 5. Строим гистограмму в виде столбиков шириной
Рисунок 1.9 - Гистограмма
Таблица 1.4 К построению эмпирических законов распределения
Таблица 1.5 Границы интервалов и их середины
6. Определим вероятность того, что результаты наблюдений xj, окажутся меньше, чем границы интервалов xгрj
где xгрj=xmaxj=xmin (j+1) Для рассматриваемого примера F0= 0; F1 =0, 025; F2= 0, 1; F3 =0, 35; F4 =0, 7; F5 =0, 925; F6 =0, 975; F7 =1. Полученные значения занесем в табл. 1.4. 7. Построим кумулятивную кривую для заданных экспериментальных данных (рис. 1.10).
Рисунок 1.10 - Кумулятивная кривая 8. Определяем точечные оценки полученных распределений экспериментальных данных: 1)среднее арифметическое 2)среднее арифметическое границ вариационного ряда 3)медиана 4)оценка дисперсии результата наблюдений 5)оценка СКО результата наблюдений 6)оценка СКО результата измерения (среднего арифметического) 7)оценка асимметрии 8)оценка эксцесса
|
.
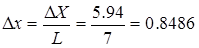
и 
и их середины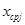 
по формулам 
и занесем их в табл. 1.5.
и высотой mj (рис. 1.9).
,
, 
, 
, 
, 
