Числовые характеристики случайной величины
Функция распределения полностью описывает случайную величину с вероятностной точки зрения. Однако на практике иногда достаточно указать отдельные параметры, характеризующие распределение случайной величины. Одними из таких характеристик являются начальные mk и центральные mk моменты различных порядков k:
Из начальных моментов на практике используется один — начальный момент первого порядка
называемый математическим ожиданием. Математическое ожидание относится к характеристикам положения, указывающим на некоторое среднее значение, вокруг которого группируются все возможные значения случайной величины. Математическое ожидание, как видно из выражения (1.6), является абсциссой центра тяжести системы материальных точек, расположенных между кривой плотности вероятности и осью абсцисс. Свойства математического ожидания: 1) математическое ожидание неслучайного числа равно самому этому числу М (а) =а; 2) постоянный множитель можно выносить за знак математического ожидания М (ах) =а М (х), где a-const; 3) математическое ожидание алгебраической суммы независимых случайных чисел равно алгебраической сумме их математических ожиданий: M (х+у-z) =M (х) + М (у) -M (z); 4) математическое ожидание произведения независимых случайных чисел равно произведению их математических ожиданий: М (х*у*z) = M (x) *M (y) *M (z); 5) математическое ожидание отклонения случайного числа от его математического ожидания равно нулю: М [х-М (х)]=0. Кроме математического ожидания к характеристикам положения относятся мода и медиана. Модой называется то значение случайной величины Mod, для которой плотность вероятности имеет максимальное значение (рис. 1.4).
Рисунок 1.4 - Математическое ожидание, мода и медиана распределения случайной величины Если плотность распределения имеет несколько максимумов, то такое распределение называется полимодальным. Иногда встречаются распределения, мода которых определяет не максимум, а минимум плотности распределения (например — арксинусное, рис. А.1, д). Такие распределения называются антимодальными. Медианой распределения случайной величины называется такое значение Me, для которого одинаково вероятно, окажется ли случайная величина больше или меньше Me, т. е. Р (х < Ме) =Р (х> Ме). Геометрическая медиана — это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 1.4). В случае симметричного одномодального распределения медиана совпадает с математическим ожиданием и модой. Из пятого свойства математического ожидания следует, что центральный момент первого порядка равен нулю. Центральный момент второго порядка, называемый дисперсией D, служит мерой рассеяния случайной величины:
Свойства дисперсии: 1) дисперсия неслучайного числа равна нулю: 2) постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат: 3) дисперсия алгебраической суммы двух зависимых случайных чисел равна
где r - коэффициент корреляции
4) дисперсия алгебраической суммы независимых случайных чисел равна сумме их дисперсий:
5) дисперсия случайного числа равна разности между математическим ожиданием его квадрата и квадратом математического ожидания:
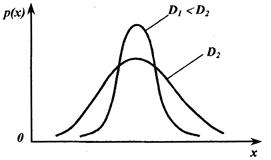
Чем больше дисперсия, тем значительнее рассеяние случайной величины (рис. 1.5).
Рисунок 1.5 - Законы распределения случайной величины с различными дисперсиями В метрологии в качестве меры рассеяния чаще используют среднее квадратическое отклонение (СКО), имеющее размерность случайной величины
Центральный момент третьего порядка является характеристикой асимметрии А:
Асимметрия может быть, положительной и отрицательной. Для симметричных распределений вероятности случайной величины асимметрия равна нулю (рис. 1.6).
Рисунок 1.6 - Законы распределения с различной асимметрией Четвертый центральный момент используется для оценки островершинности дифференциальной функции распределения вероятности. Мерой островершинности является эксцесс
В выражении (1.10) вычитание тройки производится для того, чтобы сделать эксцесс равным нулю для нормального закона распределения, для которого Таким образом, эксцесс у законов распределения вероятности будет близок к нулю, если их кривая плотности распределения будет иметь колоколообразную форму. Кривые с более острой вершиной имеют положительный эксцесс, а с более пологой — отрицательный (рис. 1.7).
Рисунок 1.7 - Законы распределения с различным эксцессом
|

 (1.4)
(1.4) (1.5)
(1.5)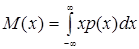 (1.6)
(1.6)
 (1.7)
(1.7) ;
; , где
, где  ;
; ,
, .
. ;
;
 (1.8)
(1.8) (1.9)
(1.9)
 (1.10)
(1.10) .
.



