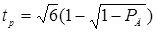Линеаризация нелинейных уравнений методом последовательных приближений
Общий метод решения этой задачи основан на допущении, что несовместность условных уравнений невелика, т.е. их невязки малы. Тогда, взяв из условной системы столько уравнений, сколько в ней неизвестных, их решением находим начальные оценки неизвестных  . Полагая далее, что . Полагая далее, что  подставляя эти выражения в условные уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок подставляя эти выражения в условные уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок  получим получим

Переписав полученное выражение в виде
 , ,
можно видеть, что мы получили условную систему линейных уравнений относительно поправок 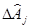 . Решение этой системы с помощью МНК . Решение этой системы с помощью МНК
дает нам их оценки и СКО. Тогда  Поскольку Поскольку  - неслучайные величины, то S2( - неслучайные величины, то S2(  ) = S2 ( ) = S2 (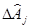 ). Получив оценки ). Получив оценки  можно сделать второе приближение и т.д. можно сделать второе приближение и т.д.

Рисунок 6.1 - Графики аппроксимирующих функций
уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок  получим получим

Переписав полученное выражение в виде
 , ,
можно видеть, что мы получили условную систему линейных уравнений относительно поправок 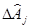 . Решение этой системы с помощью МНК . Решение этой системы с помощью МНК
дает нам их оценки и СКО. Тогда  Поскольку Поскольку  - неслучайные величины, то S2( - неслучайные величины, то S2(  ) = S2 ( ) = S2 (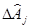 ). Получив оценки ). Получив оценки  можно сделать второе приближение и т.д. можно сделать второе приближение и т.д.
6.2 Пример выполнения контрольного задания
6.2.1 Задание
Определите вид и параметры функциональной зависимости Y=f(x, a0 a1), аппроксимирующей экспериментальную зависимость, приведенную в табл. 6.1. С доверительной вероятностью Р = 0, 95 найдите границы погрешности  и и 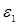 определения параметров a0 и А1 функции. определения параметров a0 и А1 функции.
6.2.2 Выполнение задания
1. Строим экспериментальную зависимость  (рис. 6.2) и по ее виду, пользуясь рис. 6.1, задаем предполагаемый функциональный вид зависимости (рис. 6.2) и по ее виду, пользуясь рис. 6.1, задаем предполагаемый функциональный вид зависимости 

Рисунок 6.2 - Экспериментальная зависимость
2. Поскольку эта зависимость нелинейная, необходимо привести ее клинейной. Для этого воспользуемся приемом линеаризации (см. п.п. 6.1.3). Вводя замену переменной 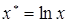 , получаем , получаем  . .
Значения х* приведены в табл. 6.1.
Строим график полученной зависимости Y = /(**) (рис. 6.3) и убеждаемся в его линейности, т.е. вид функциональной зависимости задан правильно.
3. Определим параметры a0 и А1 зависимости (6.16) методом наименьших квадратов. Для этого находим значения сумм Гаусса:  . .
Нормальная система уравнений имеет вид
416, 2 = 20  +42, 3 +42, 3 
982, 9 = 42, З  + 102, 16 + 102, 16 
Таблица 6.1.
Экспериментальные и линеаризованные зависимости
| x
| Y
| x*
| d
| Yопр
| |
| 3.62
|
| 4.18*10-5
| 3.6200
| |
| 9.25
| 0.6931
| -1.4018*10-3
| 9.2489
| |
| 12.54
| 1.0986
| 1.6*10-3
| 12.5417
| |
| 14.88
| 1.3863
| -2.033*10-3
| 14.8779
| |
| 16.69
| 1.6094
| -2.73*10-4
| 16.6900
| |
| 18.17
| 1.7918
| 9.69*10-4
| 18.1706
| |
| 19.42
| 1.9459
| 2.391*10-3
| 19.4225
| |
| 20.51
| 2.0794
| -3.477*10-3
| 20.5068
| |
| 21.46
| 2.1972
| 3.159*10-3
| 21.4634
| |
| 22.32
| 2.3026
| -9.04*10-4
| 22.3189
| |
| 23.09
| 2.3979
| 3.012*10-3
| 23.2929
| |
| 23.80
| 2.4849
| -4.75*10-4
| 23.7996
| |
| 24.45
| 2.5649
| -8.07*10-4
| 24.4498
| |
| 25.05
| 2.6391
| 1.759*10-3
| 25.0514
| |
| 25.61
| 2.7080
| 1.285*10-3
| 25.6117
| |
| 26.14
| 2.7726
| -4.108*10-3
| 26.1358
| |
| 26.63
| 2.8332
| -1.173*10-2
| 26.6281
| |
| 27.09
| 2.8904
| 2.527*10-3
| 27.0983
| |
| 27.53
| 2.9444
| 1.053*10-3
| 27.5314
| |
| 27.95
| 2.9957
| -2.348*10-3
| 27.5479
|

Рисунок 6.3 - Линеаризованная зависимость
По формулам (6. 17)-(6.19), находим  =3, 6200418; =3, 6200418;  =8, 1208432. =8, 1208432.
Подставляя оценки  , ,  в условную систему уравнений, получаем значения невязок в условную систему уравнений, получаем значения невязок  , по формуле , по формуле

Значения рассчитанных невязок  приведены в табл. 6. 1. приведены в табл. 6. 1.
4. Для определения оценок среднеквадратического отклонения  , ,  воспользуемся выражениями (6.20)-(6.21) воспользуемся выражениями (6.20)-(6.21)
 ; ;
 ; ;
 . .
Для определения границ погрешностей нахождения  , ,  воспользуемся выражением (6.22), для чего по табл. Б.5 для числа степеней свободы п -т -1=18, находим для заданной вероятности Р д=0, 95 воспользуемся выражением (6.22), для чего по табл. Б.5 для числа степеней свободы п -т -1=18, находим для заданной вероятности Р д=0, 95 
В этом случае  , ,  . .
6.3 Варианты контрольных заданий
Таблица 6.2
Варианты 1, 8, 15, 22, 29, 36, 43 ( ) )
| x
| 1)P=0.9
| 8)P=0.95
| 15)P=0.99
| 22)P=0.9
| 29)P=0.95
| 36)P=0.99
| 43)P=0.9
| |
| 10.4
| 15.7
| 32.0
| 38.8
| 14.8
| 4.02
| 4.13
| |
| 11.7
| 21.9
| 46.7
| 58.3
| 23.7
| 6.89
| 4.76
| |
| 12.9
| 28.0
| 61.4
| 77.8
| 32.7
| 9.76
| 5.41
| |
| 14.2
| 34.1
| 76.2
| 97.3
| 41.6
| 12.62
| 6.06
| |
| 15.4
| 40.2
| 90.9
| 116.8
| 50.6
| 15.49
| 6.71
| |
| 16.7
| 41.3
| 105.7
| 136.2
| 59.5
| 18.35
| 7.33
| |
| 17.9
| 52.5
| 120.4
| 155.7
| 68.5
| 21.22
| 7.97
| |
| 19.2
| 58.6
| 135.1
| 175.2
| 77.4
| 24.09
| 8.62
| |
| 20.4
| 64.7
| 149.9
| 194.7
| 86.4
| 26.95
| 9.26
| |
| 21.7
| 70.8
| 164.6
| 214.2
| 95.4
| 29.82
| 9.91
| |
| 22.9
| 77.0
| 179.4
| 233.7
| 104.3
| 32.69
| 10.54
| |
| 24.9
| 83.1
| 194.1
| 253.1
| 113.3
| 35.56
| 11.17
| |
| 25.4
| 89.2
| 208.8
| 272.6
| 122.2
| 38.43
| 11.82
| |
| 26.7
| 95.3
| 223.6
| 292.1
| 132.2
| 41.31
| 12.46
| |
| 27.9
| 101.5
| 238.3
| 311.6
| 140.2
| 44.16
| 13.1
| |
| 29.1
| 107.6
| 253.1
| 331.1
| 149.1
| 47.02
| 13.73
| |
| 30.4
| 113.7
| 267.8
| 350.6
| 158.1
| 49.89
| 14.40
| |
| 31.6
| 119.8
| 282.5
| 370.0
| 167.0
| 52.76
| 15.04
| |
| 32.9
| 125.9
| 297.3
| 389.5
| 176.0
| 55.63
| 15.67
| |
| 34.1
| 132.1
| 312.0
| 409.0
| 184.9
| 58.49
| 16.31
| Таблица 6.3
Варианты 2, 9, 16, 23, 30, 37, 44 ( ) )
| x
| 2)P=0.9
| 9)P=0.95
| 16)P=0.99
| 23)P=0.9
| 30)P=0.95
| 37)P=0.99
| 44)P=0.9
| |
| 0, 538
| 0, 38
| 1, 53
| 2, 00
| 3, 20
| 1, 91
| 37, 22
| |
| 0, 547
| 0, 91
| 1, 80
| 2, 04
| 7, 37
| 2, 25
| 27, 87
| |
| 0, 552
| 1, 51
| 1, 98
| 2, 07
| 12, 0
| 2, 65
| 20, 86
| |
| 0, 556
| 2, 15
| 2, 12
| 2, 09
| 16, 95
| 3, 12
| 15, 62
| |
| 0, 558
| 2, 84
| 2, 23
| 2, 11
| 22, 17
| 3, 67
| 11, 69
| |
| 0, 561
| 3, 55
| 2, 33
| 2, 12
| 27, 60
| 4, 32
| 8, 75
| |
| 0, 563
| 4, 30
| 2, 42
| 2, 13
| 33, 23
| 5, 08
| 6, 65
| |
| 0, 564
| 5, 07
| 2, 50
| 2, 14
| 39, 01
| 5, 98
| 4, 91
| |
| 0, 566
| 5, 87
| 2, 57
| 2, 15
| 44, 98
| 7, 04
| 3, 67
| |
| 0, 567
| 6, 08
| 2, 63
| 2, 15
| 51, 01
| 8, 27
| 2, 75
| |
| 0, 569
| 7, 62
| 2, 69
| 2, 16
| 57, 21
| 9, 73
| 2, 06
| |
| 0, 570
| 8, 32
| 2, 75
| 2, 17
| 63, 51
| 11, 45
| 1, 55
| |
| 0, 571
| 9, 24
| 2, 80
| 2, 17
| 69, 93
| 13, 47
| 1, 15
| |
| 0, 572
| 10, 13
| 2, 85
| 2, 18
| 76, 45
| 15, 85
| 0, 86
| |
| 0, 573
| 11, 03
| 2, 90
| 2, 18
| 83, 06
| 18, 64
| 0, 65
| |
| 0, 574
| 11, 94
| 2, 94
| 2, 19
| 89, 76
| 21, 93
| 0, 48
| |
| 0, 574
| 12, 87
| 2, 98
| 2, 19
| 96, 54
| 25, 80
| 0, 36
| |
| 0, 575
| 13, 81
| 3, 03
| 2, 19
| 103, 41
| 30, 35
| 0, 26
| |
| 0, 576
| 14, 77
| 3, 06
| 2, 20
| 110, 35
| 35, 70
| 0, 2
| |
| 0, 577
| 15, 73
| 3, 10
| 2, 20
| 117, 37
| 42, 00
| 0, 15
| Таблица 6.4
Варианты 3, 10, 17, 24, 31, 38, 45 ( ) )
| x
| 3)P=0.9
| 10)P=0.95
| 17)P=0.99
| 24)P=0.9
| 31)P=0.95
| 38)P=0.99
| 45)P=0.9
| |
| 8, 45
| 6, 25
| 2, 71
| 2, 10
| 1, 54
| 0, 47
| 6, 11
| |
| 9, 10
| 6, 79
| 2, 99
| 2, 33
| 1, 72
| 1, 67
| 9, 59
| |
| 9, 81
| 7, 37
| 3, 29
| 3, 58
| 1, 93
| 3, 51
| 12, 48
| |
| 10, 57
| 8, 00
| 3, 63
| 2, 86
| 2, 16
| 6, 02
| 15, 05
| |
| 11, 39
| 8, 69
| 4, 00
| 3, 17
| 2, 42
| 9, 05
| 17, 39
| |
| 12, 28
| 9, 44
| 4, 41
| 3, 51
| 2, 71
| 12, 72
| 19, 58
| |
| 13, 23
| 10, 24
| 4, 86
| 3, 89
| 3, 03
| 16, 92
| 21, 64
| |
| 14, 26
| 11, 12
| 5, 35
| 4, 31
| 3, 39
| 21, 65
| 23, 60
| |
| 15, 37
| 12, 08
| 5, 90
| 4, 78
| 3, 80
| 26, 87
| 25, 48
| |
| 16, 56
| 13, 11
| 6, 50
| 5, 30
| 4, 25
| 32, 66
| 27, 28
| |
| 17, 85
| 14, 24
| 7, 17
| 5, 78
| 4, 76
| 38, 97
| 29, 03
| |
| 19, 24
| 15, 46
| 7, 90
| 6, 51
| 5, 32
| 45, 73
| 30, 71
| |
| 20, 73
| 16, 78
| 8, 70
| 7, 21
| 5, 96
| 53, 05
| 32, 35
| |
| 22, 35
| 18, 22
| 9, 59
| 7, 99
| 6, 67
| 60, 83
| 33, 95
| |
| 24, 08
| 19, 78
| 10, 57
| 8, 86
| 7, 49
| 69, 09
| 35, 50
| |
| 25, 95
| 21, 48
| 11, 65
| 9, 82
| 8, 36
| 77, 84
| 37, 02
| |
| 27, 97
| 23, 32
| 12, 84
| 10, 88
| 9, 36
| 87, 07
| 38, 51
| |
| 30, 14
| 25, 32
| 14, 16
| 12, 06
| 10, 48
| 96, 76
| 39, 97
| |
| 32, 49
| 27, 49
| 15, 60
| 13, 37
| 11, 73
| 106, 93
| 41, 40
| |
| 35, 01
| 29, 84
| 17, 20
| 14, 82
| 13, 13
| 117, 56
| 42, 80
| Таблица 6.5
Варианты 4, 11, 18, 25, 32, 39, 46 ( ) )
| x
| 4)P=0.9
| 11)P=0.95
| 18)P=0.99
| 25)P=0.9
| 32)P=0.95
| 39)P=0.99
| 46)P=0.9
| |
| 10, 72
| 21, 90
| 18, 64
| 13, 03
| 10, 36
| 1, 63
| 15, 98
| |
| 8, 95
| 13, 69
| 13, 24
| 10, 62
| 9, 06
| 1, 71
| 13, 15
| |
| 7, 68
| 9, 96
| 10, 27
| 8, 96
| 8, 05
| 1, 79
| 11, 18
| |
| 6, 72
| 7, 82
| 8, 39
| 7, 74
| 7, 24
| 1, 88
| 9, 72
| |
| 5, 98
| 6, 44
| 7, 09
| 6, 82
| 6, 58
| 1, 98
| 8, 59
| |
| 5, 39
| 5, 48
| 6, 14
| 6, 10
| 6, 03
| 2, 09
| 7, 01
| |
| 4, 90
| 4, 76
| 5, 41
| 5, 51
| 5, 57
| 2, 22
| 6, 98
| |
| 4, 49
| 4, 21
| 4, 84
| 5, 03
| 5, 17
| 2, 36
| 6, 38
| |
| 4, 15
| 3, 78
| 4, 38
| 4, 62
| 4, 83
| 2, 52
| 5, 88
| |
| 3, 85
| 3, 42
| 4, 00
| 4, 28
| 4, 52
| 2, 71
| 5, 45
| |
| 3, 60
| 3, 13
| 3, 68
| 3, 98
| 4, 26
| 2, 92
| 5, 08
| |
| 3, 37
| 2, 88
| 3, 40
| 3, 72
| 4, 02
| 3, 17
| 4, 75
| |
| 3, 17
| 2, 67
| 3, 17
| 3, 49
| 3, 81
| 3, 46
| 4, 47
| |
| 3, 00
| 2, 49
| 2, 96
| 3, 29
| 3, 62
| 3, 82
| 4, 22
| |
| 2, 84
| 2, 33
| 2, 78
| 3, 11
| 3, 45
| 4, 27
| 3, 99
| |
| 2, 70
| 2, 19
| 2, 62
| 2, 95
| 3, 29
| 4, 82
| 3, 79
| |
| 2, 57
| 2, 07
| 2, 48
| 2, 81
| 3, 15
| 5, 54
| 3, 60
| |
| 2, 45
| 1, 96
| 2, 35
| 2, 68
| 3, 02
| 6, 52
| 3, 44
| |
| 2, 35
| 1, 86
| 2, 24
| 2, 56
| 2, 89
| 7, 91
| 3, 29
| |
| 2, 25
| 1, 77
| 2, 13
| 2, 45
| 2, 78
| 10, 05
| 3, 15
|
Таблица 6.6
Варианты 5, 12, 19, 26, 33, 40, 47 ( ) )
| x
| 5)P=0.9
| 12)P=0.95
| 19)P=0.99
| 26)P=0.9
| 33)P=0.95
| 40)P=0.99
| 47)P=0.9
| |
| 0, 229
| 0, 0818
| 0, 0381
| 1, 1104
| 133, 1
| 2, 59
| 0, 17
| |
| 0, 284
| 0, 09558
| 0, 0480
| 1, 1464
| 174, 1
| 4, 88
| 0, 35
| |
| 0, 304
| 0, 1015
| 0, 0526
| 1, 1589
| 194, 1
| 6, 91
| 0, 56
| |
| 0, 322
| 0, 1047
| 0, 0552
| 1, 1653
| 205, 7
| 8, 74
| 0, 78
| |
| 0, 331
| 0, 1066
| 0, 0569
| 1, 1692
| 213, 7
| 10, 37
| 1, 04
| |
| 0, 338
| 0, 1080
| 0, 0581
| 1, 1717
| 219, 2
| 11, 85
| 1, 33
| |
| 0, 342
| 0, 1090
| 0, 0590
| 1, 1736
| 223, 3
| 13, 20
| 1, 65
| |
| 0, 346
| 0, 1098
| 0, 0597
| 1, 1750
| 226, 5
| 14, 43
| 2, 03
| |
| 0, 349
| 0, 1104
| 0, 0602
| 1, 1761
| 229, 1
| 15, 56
| 2, 46
| |
| 0, 351
| 0, 1108
| 0, 0610
| 1, 1769
| 231, 2
| 16, 59
| 2, 97
| |
| 0, 353
| 0, 1112
| 0, 0613
| 1, 1777
| 232, 9
| 17, 55
| 3, 57
| |
| 0, 355
| 0, 1116
| 0, 0616
| 1, 1782
| 234, 4
| 18, 43
| 4, 29
| |
| 0, 356
| 0, 1119
| 0, 0618
| 1, 1787
| 235, 6
| 19, 26
| 5, 18
| |
| 0, 357
| 0, 1121
| 0, 0620
| 1, 1792
| 236, 7
| 20, 02
| 6, 29
| |
| 0, 358
| 0, 1123
| 0, 0622
| 1, 1796
| 237, 6
| 20, 73
| 7, 75
| |
| 0, 359
| 0, 1125
| 0, 0624
| 1, 1799
| 238, 5
| 21, 40
| 9, 69
| |
| 0, 360
| 0, 1127
| 0, 0625
| 1, 1802
| 239, 2
| 22, 03
| 12, 47
| |
| 0, 361
| 0, 1128
| 0, 0626
| 1, 1804
| 239, 9
| 22, 62
| 16, 71
| |
| 0, 361
| 0, 1130
| 0, 0627
| 1, 1807
| 240, 9
| 23, 99
| 24, 04
| |
| 0, 362
| 0, 1131
| 0, 0628
| 1, 1809
| 241, 1
| 23, 69
| 39, 69
| Таблица 6.7
Варианты 6, 13, 20, 27, 34, 41, 48 (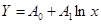 ) )
| x
| 6)P=0.9
| 13)P=0.95
| 20)P=0.99
| 27)P=0.9
| 34)P=0.95
| 41)P=0.99
| 48)P=0.9
| |
| 19, 35
| 1, 550
| 10, 383
| 1, 452
| 15, 155
| 3, 49
| 5, 14
| |
| 32, 68
| 2, 760
| 18, 324
| 14, 785
| 15, 850
| 14, 22
| 13, 36
| |
| 40, 48
| 3, 469
| 22, 969
| 22, 585
| 16, 257
| 20, 49
| 18, 17
| |
| 46, 02
| 3, 972
| 26, 265
| 28, 118
| 16, 546
| 24, 95
| 21, 58
| |
| 50, 31
| 4, 362
| 28, 821
| 32, 411
| 16, 769
| 28, 41
| 24, 23
| |
| 53, 82
| 4, 681
| 30, 910
| 35, 917
| 17, 952
| 31, 23
| 26, 39
| |
| 56, 78
| 4, 951
| 32, 676
| 38, 883
| 17, 107
| 33, 61
| 28, 22
| |
| 59, 35
| 5, 184
| 34, 205
| 41, 451
| 17, 241
| 35, 68
| 29, 80
| |
| 61, 62
| 5, 339
| 35, 555
| 43, 717
| 17, 359
| 37, 51
| 31, 20
| |
| 63, 64
| 5, 574
| 36, 762
| 45, 744
| 17, 465
| 39, 14
| 32, 45
| |
| 65, 68
| 5, 741
| 37, 854
| 47, 577
| 17, 561
| 40, 61
| 33, 58
| |
| 67, 15
| 5, 893
| 38, 851
| 49, 251
| 17, 641
| 41, 96
| 34, 61
| |
| 68, 69
| 6, 034
| 39, 768
| 50, 779
| 17, 728
| 43, 19
| 35, 56
| |
| 70, 12
| 6, 163
| 40, 617
| 52, 216
| 17, 803
| 44, 35
| 36, 44
| |
| 71, 45
| 6, 283
| 41, 407
| 53, 541
| 17, 872
| 45, 41
| 37, 26
| |
| 72, 68
| 6, 396
| 42, 164
| 54, 786
| 17, 937
| 46, 41
| 38, 03
| |
| 73, 85
| 6, 502
| 42, 841
| 55, 951
| 17, 997
| 47, 35
| 38, 75
| |
| 74, 95
| 6, 603
| 43, 496
| 57, 050
| 18, 055
| 48, 23
| 39, 42
| |
| 76, 99
| 6, 697
| 44, 115
| 58, 090
| 18, 109
| 49, 07
| 40, 06
| |
| 76, 98
| 6, 786
| 44, 703
| 59, 076
| 18, 160
| 49, 87
| 40, 67
| Таблица 6.8
Варианты 7, 14, 21, 28, 35, 42, 49 ( ) )
| x
| 7)P=0.9
| 14)P=0.95
| 21)P=0.99
| 28)P=0.9
| 35)P=0.95
| 42)P=0.99
| 49)P=0.9
| |
| 21, 68
| 29, 03
| 29, 88
| 22, 63
| 43, 22
| 21, 71
| 27, 89
| |
| 12, 71
| 11, 56
| 16, 37
| 14, 73
| 16, 74
| 12, 61
| 16, 34
| |
| 9, 72
| 5, 74
| 11, 86
| 12, 10
| 7, 91
| 9, 58
| 12, 49
| |
| 8, 23
| 2, 83
| 9, 61
| 10, 78
| 3, 50
| 8, 07
| 10, 57
| |
| 7, 33
| 1, 08
| 8, 26
| 9, 98
| 0, 85
| 7, 16
| 9, 41
| |
| 6, 73
| -0, 09
| 7, 36
| 9, 46
| -0, 92
| 6, 55
| 8, 64
| |
| 6, 30
| -0, 92
| 6, 72
| 9, 09
| -2, 18
| 6, 12
| 8, 09
| |
| 5, 98
| -1, 54
| 6, 23
| 8, 80
| -3, 12
| 5, 79
| 7, 68
| |
| 5, 73
| -2, 03
| 5, 86
| 8, 58
| -3, 86
| 5, 54
| 7, 36
| |
| 5, 53
| -2, 41
| 5, 56
| 8, 41
| -4, 45
| 5, 34
| 7, 10
| |
| 5, 37
| -2, 73
| 5, 31
| 8, 26
| -4, 93
| 5, 17
| 6, 89
| |
| 5, 24
| -3, 00
| 5, 11
| 8, 14
| -5, 33
| 5, 03
| 6, 72
| |
| 5, 12
| -3, 22
| 4, 94
| 8, 04
| -5, 67
| 4, 92
| 6, 57
| |
| 5, 02
| -3, 41
| 4, 79
| 7, 96
| -5, 96
| 4, 82
| 6, 44
| |
| 4, 94
| -3, 58
| 4, 66
| 7, 88
| -6, 21
| 4, 73
| 6, 33
| |
| 4, 86
| -3, 72
| 4, 55
| 7, 82
| -6, 43
| 4, 65
| 6, 23
| |
| 4, 80
| -3, 85
| 4, 45
| 7, 76
| -6, 63
| 4, 58
| 6, 15
| |
| 4, 74
| -3, 97
| 4, 36
| 7, 71
| -6, 80
| 4, 53
| 6, 07
| |
| 4, 68
| -4, 07
| 4, 28
| 7, 66
| -6, 96
| 4, 48
| 6, 01
| |
| 4, 64
| -4, 16
| 4, 21
| 7, 62
| -7, 09
| 4, 43
| 5, 94
|
Приложение А - Законы распределения случайных величин
Равновероятное распределение (рис. А1, а).
Плотность распределения

Интегральная функция распределения

Параметры А - 0; E - -1, 2; tp= 
Треугольное распределение (Симпсона) (рис. А1, б).
Плотность распределения

Интегральная функция распределения

Параметры A = 0; Е = -0, 6;  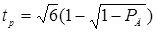
Нормальный закон (Гаусса) (рис. А1, в).
Плотность распределения


Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Вопрос 1. Коллективные средства защиты: вентиляция, освещение, защита от шума и вибрации Коллективные средства защиты: вентиляция, освещение, защита от шума и вибрации
К коллективным средствам защиты относятся: вентиляция, отопление, освещение, защита от шума и вибрации...
Задержки и неисправности пистолета Макарова 1.Что может произойти при стрельбе из пистолета, если загрязнятся пазы на рамке...
Вопрос. Отличие деятельности человека от поведения животных главные отличия деятельности человека от активности животных сводятся к следующему: 1...
|
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
|
|

 . Полагая далее, что
. Полагая далее, что  подставляя эти выражения в условные уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок
подставляя эти выражения в условные уравнения, раскладываем условные уравнения в ряды. Сохраняя лишь члены с первыми степенями поправок  получим
получим
 ,
,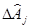 . Решение этой системы с помощью МНК
. Решение этой системы с помощью МНК Поскольку
Поскольку  - неслучайные величины, то S2(
- неслучайные величины, то S2(  ) = S2 (
) = S2 (
 ,
, и
и 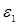 определения параметров a0 и А1 функции.
определения параметров a0 и А1 функции. (рис. 6.2) и по ее виду, пользуясь рис. 6.1, задаем предполагаемый функциональный вид зависимости
(рис. 6.2) и по ее виду, пользуясь рис. 6.1, задаем предполагаемый функциональный вид зависимости 

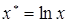 , получаем
, получаем  .
. .
. +42, 3
+42, 3  + 102, 16
+ 102, 16 

 =8, 1208432.
=8, 1208432. , по формуле
, по формуле
 приведены в табл. 6. 1.
приведены в табл. 6. 1. ;
; ;
; .
.
 ,
,  .
. )
) )
) )
) )
) )
)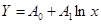 )
) )
)