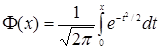Интегральная функция распределения
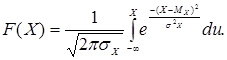
Параметры A = 0; E = 0; 
Двойное экспоненциальное распределение (Лапласа) (рис. А1, г).
Плотность распределения
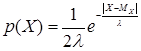
Интегральная функция распределения
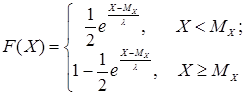
Параметры 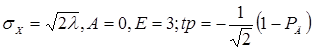
Распределение по закону арксинуса (рис. А.1, д).
Плотность распределения
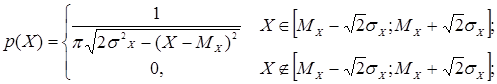
Интегральная функция распределения
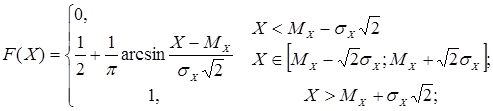
Параметры А = 0; E = -1, 5;  . .
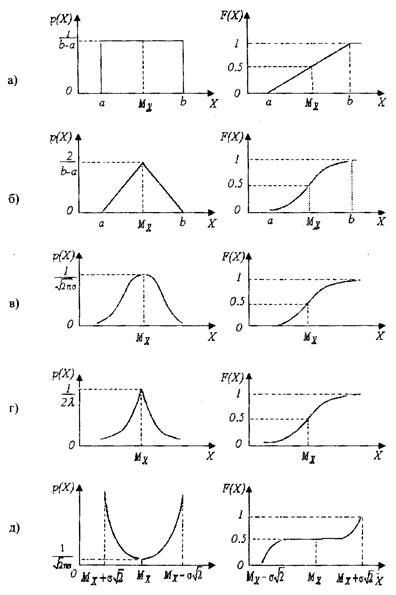
а – равновероятный, в – треугольный (Симпсон), в – нормальный (Гаусса),
двойной экспоненциальный (Лапласа), д) арксинуса
Рисунок А.1. Законы распределения
Приложение Б –Статистические таблицы
Таблица Б1
Зависимость b(n) в критерии Смирнова
| n
| Нормальный
| Арксинус
| Равномерный
| Треугольный
| Лаплас
|
| | 0, 9
| 0, 95
| 0, 99
| 0, 9
| 0, 95
| 0, 99
| 0, 9
| 0, 95
| 0, 99
| 0, 9
| 0, 95
| 0, 99
| 0, 9
| 0, 95
| 0, 99
| |
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| 1, 41
| |
| 1, 87
| 1, 92
| 1, 97
| 1, 90
| 1, 95
| 2, 00
| 1, 87
| 1, 91
| 1, 98
| 1, 86
| 1, 91
| 1, 97
| 1, 91
| 1, 95
| 1, 98
| |
| 2, 09
| 2, 18
| 2, 31
| 2, 01
| 2, 14
| 2, 34
| 2, 02
| 2, 14
| 2, 30
| 2, 06
| 2, 15
| 2, 30
| 2, 22
| 2, 30
| 2, 39
| |
| 2, 24
| 2, 35
| 2, 53
| 2, 03
| 2, 17
| 2, 45
| 2, 07
| 2, 19
| 2, 46
| 2, 17
| 2, 29
| 2, 44
| 2, 43
| 2, 55
| 2, 69
| |
| 2, 34
| 2, 47
| 2, 69
| 2, 00
| 2, 16
| 2, 45
| 2, 09
| 2, 21
| 2, 52
| 2, 23
| 2, 35
| 2, 53
| 2, 60
| 2, 73
| 2, 91
| |
| 2, 43
| 2, 56
| 2, 81
| 1, 97
| 2, 13
| 2, 41
| 2, 10
| 2, 22
| 2, 53
| 2, 26
| 2, 40
| 2, 60
| 2, 76
| 2, 92
| 3, 11
| |
| 2, 53
| 2, 67
| 2, 95
| 1, 94
| 2, 09
| 2, 38
| 2, 10
| 2, 23
| 2, 52
| 2, 29
| 2, 44
| 2, 64
| 2, 90
| 3, 06
| 3, 30
| |
| 2, 55
| 2, 70
| 2, 98
| 1, 91
| 2, 06
| 2, 34
| 2, 09
| 2, 22
| 2, 49
| 2, 32
| 2, 47
| 2, 67
| 2, 98
| 3, 18
| 3, 46
| |
| 2, 60
| 2, 75
| 3, 05
| 1, 98
| 2, 01
| 2, 31
| 2, 09
| 2, 21
| 2, 48
| 2, 34
| 2, 49
| 2, 70
| 3, 09
| 3, 28
| 3, 60
| |
| 2, 64
| 2, 80
| 3, 10
| 1, 86
| 1, 99
| 2, 27
| 2, 08
| 2, 19
| 2, 47
| 2, 36
| 2, 50
| 2, 71
| 3, 17
| 3, 37
| 3, 71
| |
| 2, 68
| 2, 84
| 3, 16
| 1, 85
| 1, 98
| 2, 25
| 2, 08
| 2, 16
| 2, 46
| 2, 38
| 2, 51
| 2, 72
| 3, 26
| 3, 46
| 3, 82
| |
| 2, 72
| 2, 88
| 3, 20
| 1, 84
| 1, 97
| 2, 22
| 2, 07
| 2, 15
| 2, 45
| 2, 39
| 2, 51
| 2, 73
| 3, 35
| 3, 55
| 3, 91
| |
| 2, 75
| 2, 91
| 3, 24
| 1, 83
| 1, 96
| 2, 21
| 2, 06
| 2, 15
| 2, 44
| 2, 40
| 2, 52
| 2, 73
| 3, 39
| 3, 63
| 4, 00
| |
| 2, 78
| 2, 94
| 3, 28
| 1, 82
| 1, 95
| 2, 19
| 2, 06
| 2, 15
| 2, 43
| 2, 41
| 2, 52
| 2, 73
| 3, 48
| 3, 70
| 4, 09
| |
| 2, 81
| 2, 97
| 3, 31
| 1, 81
| 1, 94
| 2, 18
| 2, 05
| 2, 14
| 2, 42
| 2, 41
| 2, 52
| 2, 74
| 3, 52
| 3, 76
| 4, 18
| |
| 2, 83
| 3, 00
| 3, 34
| 1, 80
| 1, 93
| 2, 17
| 2, 05
| 2, 14
| 2, 40
| 2, 42
| 2, 53
| 2, 74
| 3, 59
| 3, 82
| 4, 26
| |
| 2, 85
| 3, 02
| 3, 36
| 1, 79
| 1, 92
| 2, 16
| 2, 04
| 2, 14
| 2, 39
| 2, 42
| 2, 53
| 2, 74
| 3, 64
| 3, 88
| 4, 33
| |
| 2, 87
| 3, 04
| 3, 39
| 1, 78
| 1, 91
| 2, 15
| 2, 04
| 2, 13
| 2, 38
| 2, 43
| 2, 53
| 2, 75
| 3, 68
| 3, 93
| 4, 39
| |
| 2, 89
| 3, 06
| 3, 41
| 1, 77
| 1, 90
| 2, 14
| 2, 03
| 2, 13
| 2, 37
| 2, 43
| 2, 53
| 2, 75
| 3, 73
| 3, 98
| 4, 45
| |
| 2, 91
| 3, 08
| 3, 43
| 1, 77
| 1, 90
| 2, 14
| 2, 03
| 2, 13
| 2, 36
| 2, 44
| 2, 53
| 2, 75
| 3, 78
| 4, 03
| 4, 50
| | | | | | | | | | | | | | | | | | | Таблица Б2
Зависимость вероятности Р0 от  l в критерии Смирнова l в критерии Смирнова
| P0
| 1.000
| 1.000
| 1.000
| 1.000
| 0.997
| 0.964
| 0.864
| | l
| 0.0
| 0.1
| 0.2
| 0.3
| 0.4
| 0.5
| 0.6
|
Таблица Б3
Значения  для различных К и Р0 в критерии Пирсона для различных К и Р0 в критерии Пирсона
| K=L-3
| Заданная вероятность P0
| | 0, 90
| 0, 95
| 0, 99
| 0, 999
| |
| 2, 71
| 3, 84
| 6, 64
| 10, 83
| |
| 4, 60
| 5, 99
| 9, 31
| 13, 82
| |
| 6, 22
| 7, 82
| 11, 35
| 16, 27
| |
| 7, 78
| 9, 49
| 13, 28
| 18, 46
| |
| 9, 24
| 11, 07
| 15, 09
| 20, 50
| |
| 10, 65
| 12, 59
| 16, 81
| 22, 50
| |
| 12, 02
| 14, 07
| 19, 47
| 24, 30
| |
| 13, 36
| 15, 51
| 20, 1
| 26, 10
| |
| 14, 68
| 16, 92
| 21, 7
| 27, 90
| |
| 15, 99
| 18, 31
| 23, 2
| 29, 60
| Таблица Б4
Статистика величины d в составном критерии
а) нормальный
| n
| P=0.9
| P=0.95
| P=0.99
| | dmin
| dmax
| dmin
| dmax
| dmin
| dmax
| |
| 0.7409
| 0.8899
| 0.7153
| 0.9073
| 0.6675
| 0.9359
| |
| 0.7452
| 0.8733
| 0.7263
| 0.8884
| 0.6829
| 0.9137
| |
| 0.7495
| 0.8631
| 0.7304
| 0.8768
| 0.6950
| 0.9001
| |
| 0.7530
| 0.8570
| 0.7360
| 0.8686
| 0.7040
| 0.8901
| |
| 0.7559
| 0.8511
| 0.7404
| 0.8625
| 0.7110
| 0.6827
| |
| 0.7583
| 0.8468
| 0.7440
| 0.5778
| 0.7167
| 0.8769
| |
| 0.7604
| 0.8436
| 0.7470
| 0.8540
| 0.7216
| 0.8722
| |
| 0.7621
| 0.8409
| 0.7496
| 0.8508
| 0.7256
| 0.8682
| |
| 0.7636
| 0.8385
| 0.7518
| 0.8481
| 0.7291
| 0.8648
| б) равномерный
| n
| P=0.9
| P=0.95
| P=0.99
| | dmin
| dmax
| dmin
| dmax
| dmin
| dmax
| |
| 0, 7726
| 0, 9347
| 0, 7435
| 0, 9438
| 0, 7016
| 0, 9593
| |
| 0, 7860
| 0, 9277
| 0, 7696
| 0, 9375
| 0, 7379
| 0, 9556
| |
| 0, 8009
| 0, 9181
| 0, 7879
| 0, 9251
| 0, 7617
| 0, 9433
| |
| 0, 8067
| 0, 9119
| 0, 7958
| 0, 9198
| 0, 7706
| 0, 9325
| |
| 0, 8166
| 0, 9103
| 0, 8056
| 0, 9187
| 0, 7826
| 0, 9312
| |
| 0, 8178
| 0, 9066
| 0, 8095
| 0, 9137
| 0, 7964
| 0, 9248
| |
| 0, 8219
| 0, 9047
| 0, 8500
| 0, 9103
| 0, 7997
| 0, 9208
| |
| 0, 8258
| 0, 9014
| 0, 8197
| 0, 9069
| 0, 8007
| 0, 9172
| |
| 0, 8298
| 0, 8995
| 0, 8242
| 0, 9054
| 0, 8053
| 0, 9177
|
в) треугольный
| n
| P=0.9
| P=0.95
| P=0.99
| | dmin
| dmax
| dmin
| dmax
| dmin
| dmax
| |
| 0, 7292
| 0, 9117
| 0, 7067
| 0, 9238
| 0, 6638
| 0, 9455
| |
| 0, 7367
| 0, 8946
| 0, 7183
| 0, 9093
| 0, 6781
| 0, 9359
| |
| 0, 7514
| 0, 8822
| 0, 7343
| 0, 8913
| 0, 7091
| 0, 9119
| |
| 0, 7604
| 0, 8771
| 0, 7430
| 0, 8867
| 0, 7203
| 0, 9049
| |
| 0, 7657
| 0, 8719
| 0, 7536
| 0, 8817
| 0, 7282
| 0, 8977
| |
| 0, 7671
| 0, 8678
| 0, 7550
| 0, 8768
| 0, 7315
| 0, 8901
| |
| 0, 7707
| 0, 8618
| 0, 7608
| 0, 8719
| 0, 7409
| 0, 8859
| |
| 0, 7735
| 0, 8601
| 0, 7628
| 0, 8689
| 0, 7433
| 0, 8800
| |
| 0, 7747
| 0, 8599
| 0, 7729
| 0, 8678
| 0, 7423
| 0, 8770
| г) Лаплас
| n
| P=0.9
| P=0.95
| P=0.99
| | dmin
| dmax
| dmin
| dmax
| dmin
| dmax
| |
| 0, 6313
| 0, 8790
| 0, 6187
| 0, 8966
| 0, 5713
| 0, 9226
| |
| 0, 6362
| 0, 8556
| 0, 6217
| 0, 8718
| 0, 5729
| 0, 9139
| |
| 0, 6371
| 0, 8400
| 0, 6231
| 0, 8573
| 0, 5741
| 0, 8809
| |
| 0, 6383
| 0, 8277
| 0, 6250
| 0, 8399
| 0, 5769
| 0, 8702
| |
| 0, 6431
| 0, 8145
| 0, 6259
| 0, 8272
| 0, 5793
| 0, 8675
| |
| 0, 6439
| 0, 8068
| 0, 6268
| 0, 8236
| 0, 5896
| 0, 8519
| |
| 0, 6458
| 0, 8022
| 0, 6285
| 0, 8147
| 0, 5900
| 0, 8458
| |
| 0, 6463
| 0, 7967
| 0, 6313
| 0, 8069
| 0, 5907
| 0, 8324
| |
| 0, 6486
| 0, 7941
| 0, 6341
| 0, 8061
| 0, 6073
| 0, 8125
| д) арксинус
| n
| P=0.9
| P=0.95
| P=0.99
| | dmin
| dmax
| dmin
| dmax
| dmin
| dmax
| |
| 0, 7937
| 0, 9558
| 0, 7680
| 0, 9664
| 0, 7226
| 0, 9803
| |
| 0, 8098
| 0, 9519
| 0, 7922
| 0, 9616
| 0, 7529
| 0, 9765
| |
| 0, 8290
| 0, 9427
| 0, 8179
| 0, 9512
| 0, 7773
| 0, 9661
| |
| 0, 8376
| 0, 9382
| 0, 8260
| 0, 9459
| 0, 7965
| 0, 9633
| |
| 0, 8466
| 0, 9340
| 0, 8352
| 0, 9433
| 0, 8109
| 0, 9586
| |
| 0, 8478
| 0, 9318
| 0, 8385
| 0, 9403
| 0, 8167
| 0, 9545
| |
| 0, 8524
| 0, 9304
| 0, 8444
| 0, 9364
| 0, 8219
| 0, 9526
| |
| 0, 8561
| 0, 9293
| 0, 8477
| 0, 9361
| 0, 8246
| 0, 9516
| |
| 0, 8622
| 0, 9273
| 0, 8530
| 0, 9329
| 0, 8383
| 0, 9510
|
Таблица Б5
Коэффициент распределения Стьюдента для числа измерений n
| n
| Доверительная вероятность P
| | 0.9
| 0.95
| 0.99
| 0.999
| |
| 6.31
| 12.71
| 63.68
| 636.62
| |
| 2.92
| 4.30
| 9.93
| 31.60
| |
| 2.35
| 3.18
| 5.84
| 12.92
| |
| 2.13
| 2.78
| 4.60
| 8.61
| |
| 2.02
| 2.57
| 4.06
| 6.87
| |
| 1.94
| 2.45
| 3.71
| 5.96
| |
| 1.9
| 2.37
| 3.50
| 5.41
| |
| 1.86
| 2.31
| 3.36
| 5.04
| |
| 1.83
| 2.26
| 3.25
| 4.78
| |
| 1.81
| 2.23
| 3.17
| 4.59
| |
| 1.80
| 2.20
| 3.11
| 4.44
| |
| 1.78
| 2.18
| 3.06
| 4.32
| |
| 1.77
| 2.16
| 3.01
| 4.22
| |
| 1.76
| 2.15
| 2.98
| 4.14
| |
| 1.75
| 2.13
| 2.95
| 4.07
| |
| 1.75
| 2.12
| 2.92
| 4.02
| |
| 1.74
| 2.11
| 2.90
| 3.97
| |
| 1.73
| 2.10
| 2.88
| 3.92
| |
| 1.73
| 2.09
| 2.86
| 3.88
| | ¥
| 1.65
| 1.96
| 2.58
| 3.29
|
Таблица Б6
Функция Лапласа 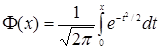
| z
| Ф(z)
| z
| Ф(z)
| z
| Ф(z)
| z
| Ф(z)
| | 0.00
| 0.0000
| 0.60
| 0.2257
| 1.20
| 0.3849
| 1.80
| 0.4641
| | 0.02
| 0.0080
| 0.62
| 0.2324
| 1.22
| 0.3888
| 1.82
| 0.4656
| | 0.04
| 0.0160
| 0.64
| 0.2389
| 1.24
| 0.3925
| 1.84
| 0.4671
| | 0.06
| 0.0239
| 0.66
| 0.2454
| 1.26
| 0.3962
| 1.86
| 0.4686
| | 0.08
| 0.0319
| 0.68
| 0.2517
| 1.28
| 0.3997
| 1.88
| 0.4699
| | 0.10
| 0.0398
| 0.70
| 0.2580
| 1.30
| 0.4032
| 1.90
| 0.4713
| | 0.12
| 0.0478
| 0.72
| 0.2642
| 1.32
| 0.4066
| 1.92
| 0.4726
| | 0.14
| 0.0557
| 0.74
| 0.2703
| 1.34
| 0.4099
| 1.94
| 0.4738
| | 0.16
| 0.0636
| 0.76
| 0.2764
| 1.36
| 0.4131
| 1.96
| 0.4750
| | 0.18
| 0.0714
| 0.78
| 0.2823
| 1.38
| 0.4162
| 1.98
| 0.4761
| | 0.20
| 0.0793
| 0.80
| 0.2881
| 1.40
| 0.4192
| 2.00
| 0.4772
| | 0.22
| 0.0871
| 0.82
| 0.2939
| 1.42
| 0.4222
| 2.05
| 0.4798
| | 0.24
| 0.0948
| 0.84
| 0.2995
| 1.44
| 0.4251
| 2.10
| 0.4821
| | 0.26
| 0.1026
| 0.86
| 0.3051
| 1.46
| 0.4279
| 2.15
| 0.4842
| | 0.28
| 0.1103
| 0.88
| 0.3106
| 1.48
| 0.4306
| 2.20
| 0.4860
| | 0.30
| 0.1179
| 0.90
| 0.3159
| 1.50
| 0.4332
| 2.25
| 0.4877
| | 0.32
| 0.1255
| 0.92
| 0.3212
| 1.52
| 0.4357
| 2.30
| 0.4892
| | 0.34
| 0.1331
| 0.94
| 0.3264
| 1.54
| 0.4382
| 2.35
| 0.4906
| | 0.36
| 0.1406
| 0.96
| 0.3315
| 1.56
| 0.4406
| 2.40
| 0.4918
| | 0.38
| 0.1480
| 0.98
| 0.3365
| 1.58
| 0.4429
| 2.45
| 0.4928
| | 0.40
| 0.1554
| 1.00
| 0.3413
| 1.60
| 0.4452
| 2.50
| 0.4938
| | 0.42
| 0.1628
| 1.02
| 0.3461
| 1.62
| 0.4474
| 2.60
| 0.4953
| | 0.44
| 0.1700
| 1.04
| 0.3508
| 1.64
| 0.4495
| 2.70
| 0.4965
| | 0.46
| 0.1772
| 1.06
| 0.3554
| 1.66
| 0.4515
| 2.80
| 0.4974
| | 0.48
| 0.1844
| 1.08
| 0.3599
| 1.68
| 0.4535
| 2.90
| 0.4981
| | 0.50
| 0.1915
| 1.10
| 0.3643
| 1.70
| 0.4554
| 3.00
| 0.4986
| | 0.52
| 0.1985
| 1.12
| 0.3686
| 1.72
| 0.4573
| 3.20
| 0.4993
| | 0.54
| 0.2054
| 1.14
| 0.3729
| 1.74
| 0.4591
| 3.40
| 0.4996
| | 0.56
| 0.2123
| 1.16
| 0.3770
| 1.76
| 0.4608
| 3.60
| 0.4998
| | 0.58
| 0.2190
| 1.18
| 0.3810
| 1.78
| 0.4625
| 3.80
| 0.4999
|
Таблица Б7
Значения (1-Р) ¾ процентных точек распределения Фишера
| K2
| P
| K1
| |
|
|
|
|
|
|
|
|
| ¥
| |
| 0.9
| 4.11
| 3.94
| 3.88
| 3.84
| 3.83
| 3.82
| 3.80
| 3.79
| 3.78
| 3.76
| | 0.95
| 6.39
| 6.00
| 5.87
| 5.81
| 5.77
| 5.75
| 5.72
| 5.70
| 5.66
| 5.63
| | 0.99
| 16.0
| 14.7
| 14.2
| 14.0
| 13.9
| 13.9
| 13.8
| 13.7
| 13.6
| 13.5
| |
| 0.9
| 2.69
| 2.44
| 2.35
| 2.31
| 2.28
| 2.26
| 2.23
| 2.22
| 2.19
| 2.16
| | 0.95
| 4.26
| 3.18
| 3.02
| 2.95
| 2.90
| 2.87
| 2.83
| 2.80
| 2.76
| 2.71
| | 0.99
| 8.02
| 5.35
| 5.00
| 4.84
| 4.73
| 4.66
| 4.57
| 4.52
| 4.42
| 4.31
| |
| 0.9
| 2.39
| 2.12
| 2.02
| 1.97
| 1.94
| 1.92
| 1.89
| 1.87
| 1.83
| 1.80
| | 0.95
| 3.11
| 2.65
| 2.48
| 2.40
| 2.35
| 2.31
| 2.27
| 2.24
| 2.19
| 2.13
| | 0.99
| 5.56
| 4.03
| 3.70
| 3.54
| 3.43
| 3.36
| 3.27
| 3.22
| 3.11
| 3.00
| |
| 0.9
| 2.27
| 1.98
| 1.88
| 1.82
| 1.79
| 1.76
| 1.73
| 1.71
| 1.67
| 1.63
| | 0.95
| 2.90
| 2.42
| 2.26
| 2.17
| 2.11
| 2.08
| 2.03
| 2.00
| 1.94
| 1.88
| | 0.99
| 4.50
| 3.53
| 3.19
| 3.03
| 2.93
| 2.86
| 2.77
| 2.71
| 2.60
| 2.49
| |
| 0.9
| 2.19
| 1.91
| 1.80
| 1.74
| 1.70
| 1.68
| 1.64
| 1.62
| 1.58
| 1.53
| | 0.95
| 2.78
| 2.30
| 2.13
| 2.05
| 1.98
| 1.95
| 1.90
| 1.86
| 1.80
| 1.73
| | 0.99
| 4.22
| 3.26
| 2.93
| 2.77
| 2.66
| 2.59
| 2.50
| 2.44
| 2.33
| 2.21
| |
| 0.9
| 2.15
| 1.86
| 1.75
| 1.69
| 1.65
| 1.62
| 1.59
| 1.56
| 1.52
| 1.47
| | 0.95
| 2.70
| 2.22
| 2.05
| 1.96
| 1.90
| 1.86
| 1.81
| 1.78
| 1.71
| 1.64
| | 0.99
| 4.04
| 3.09
| 2.77
| 2.60
| 2.49
| 2.43
| 2.33
| 2.28
| 2.16
| 2.03
| |
| 0.9
| 2.10
| 1.79
| 1.68
| 1.62
| 1.58
| 1.55
| 1.52
| 1.49
| 1.44
| 1.39
| | 0.95
| 2.61
| 2.13
| 1.95
| 1.86
| 1.79
| 1.76
| 1.70
| 1.67
| 1.60
| 1.52
| | 0.99
| 3.83
| 2.89
| 2.57
| 2.41
| 2.29
| 2.22
| 2.14
| 2.08
| 1.95
| 1.82
| |
| 0.9
| 2.09
| 1.74
| 1.68
| 1.58
| 1.52
| 1.49
| 1.46
| 1.45
| 1.40
| 1.34
| | 0.95
| 2.56
| 2.07
| 1.90
| 1.78
| 1.74
| 1.66
| 1.64
| 1.61
| 1.54
| 1.40
| | 0.99
| 3.73
| 2.79
| 2.47
| 2.28
| 2.19
| 2.11
| 2.02
| 1.96
| 1.85
| 1.62
| |
| 0.9
| 2.00
| 1.70
| 1.58
| 1.51
| 1.47
| 1.44
| 1.39
| 1.37
| 1.30
| 1.22
| | 0.95
| 2.46
| 1.97
| 1.79
| 1.60
| 1.63
| 1.59
| 1.50
| 1.49
| 1.39
| 1.28
| | 0.99
| 3.51
| 2.59
| 2.26
| 2.10
| 1.98
| 1.93
| 1.80
| 1.74
| 1.59
| 1.43
| |
¥
| 0.9
| 1.94
| 1.63
| 1.51
| 1.43
| 1.38
| 1.35
| 1.30
| 1.26
| 1.18
| 1.00
| | 0.95
| 2.37
| 1.88
| 1.69
| 1.59
| 1.52
| 1.47
| 1.40
| 1.35
| 1.24
| 1.00
| | 0.99
| 3.32
| 2.41
| 2.07
| 1.91
| 1.79
| 1.72
| 1.60
| 1.53
| 1.36
| 1.00
|
СПИСОК ЛИТЕРАТУРЫ
1. Грановский В.А., Сирая Т.Н. Методы обработки экспериментальных данных при измерениях. - Л.: Энергоатомиздат. Ленингр. отд-ние, 1990.-288с.
2. Долинский Е.Ф. Обработка результатов измерений М.: Изд-во стандартов, 1973.-192 с.
3. Захаров И.П. Теоретическая метрология. - Харьков: ХТУРЭ, 2000.-.172 с.
4. Кукуш В.Д. Определение погрешностей результатов и средств измерений. - Харьков: ХПИ, 1979. -116с.
5. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов из-цяерений. - Л.: Энергоатомиздат, 1985. - 248 с.
6. Рабинович С.Г. Погрешности измерений. - Л.: Энергия. Ленинградское отд-ние, 1978.- 262 с.
7. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. - М.: Машиностроение, 1985.- 232 с.
8. Фильчаков П.Ф. Численные и графические методы прикладной математики. Справочник. - Киев: Наук. Думка, 1970.- 800 с.
9. Фрумкин В.Д., Рубичев Н.А. Теория вероятности и статистика в метрологии и измерительной технике М.: Машиностроение, 1987.- 168с.

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Что такое пропорции?
Это соотношение частей целого между собой. Что может являться частями в образе или в луке...
Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста.
Врачи-хирурги выяснили...
ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...
|
ТЕОРИЯ ЗАЩИТНЫХ МЕХАНИЗМОВ ЛИЧНОСТИ В современной психологической литературе встречаются различные термины, касающиеся феноменов защиты...
Этические проблемы проведения экспериментов на человеке и животных В настоящее время четко определены новые подходы и требования к биомедицинским исследованиям...
Классификация потерь населения в очагах поражения в военное время Ядерное, химическое и бактериологическое (биологическое) оружие является оружием массового поражения...
|
|

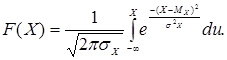

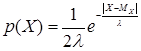
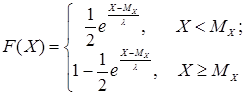
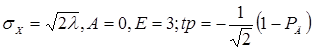
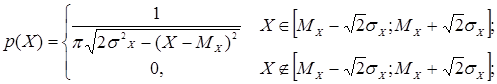
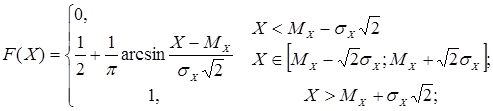
 .
.
 l в критерии Смирнова
l в критерии Смирнова для различных К и Р0 в критерии Пирсона
для различных К и Р0 в критерии Пирсона