Решение задачи с использованием системы Mathcad. Ввод текста на всех этапах решения задачи будем осуществлять с помощью комбинации клавиш Shift+" (двойная кавычка)

Ввод текста на всех этапах решения задачи будем осуществлять с помощью комбинации клавиш Shift+" (двойная кавычка), что позволит создать текстовую область. Введем на рабочем листе первый пункт расчета (рис. 5.1.2). Он будет выглядеть так:

1. Задание исходных данных одноканальной замкнутой СМО. Последовательно введем исходные данные:

- интенсивность обслуживания требований μ: = 29;

- интенсивность поступления одного требования на обслуживание λ: = 6;

- число требований, функционирующих в системе, m: = 5.

Для решения задачи воспользуемся блоком функций Given... Find. Его применение требует предварительного задания начальных приближений. Введем на рабочем листе второй пункт расчета (рис. 5.1.2). Он будет выглядеть так:

2. Начальные приближения.

Последовательно наберем начальные приближенные значения искомых параметров:

Р₀: =0, 25 Р.: -0, 15 Р₂: =0, 15 Р₃: -0, 15 Р₄: =ОД5 Р₅: =0, 15

Сумма вероятностей всех состояний должна быть равна 1. Введем на рабочем листе третий пункт расчета (рис. 5.1.2). Он будет выглядеть так:

3. Запись системы уравнений, описывающей функционирование одноканалъной СМО. Вначале записывается ключевое слово Given (Дано), которое может быть напечатано прописными, строчными буквами или начинаться с прописной.

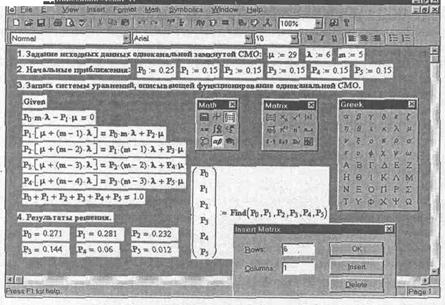
Рис 5.1.2. Определение параметров функционирования одноканальной замкнутой СМО в системе Mathcad

 

Ниже вводится исходная система уравнений.

Для примера ограничимся рассмотрением одноканальной замкнутой системы, в которой обслуживаются пять требований. Интенсивность поступления одного требования на обслуживание λ равна трем поступлениям в час. Интенсивность обслуживания в канале μ составляет 29 обслуживании в час. Эта система алгебраических уравнений будет выглядеть так:

 

P₀ mλ =P₁ μ

P₁ (μ +(m-1)λ)= P₀m λ + P₂ μ

P₂ (μ +(m-2) λ) = P₁(m-1) λ + P₃ μ

………………………………

P₄ (μ +(m-4) λ) = P ₃(m-3) λ + P ₅ μ

P₅ μ =P₄ λ

 

Однако в представленном виде определитель системы будет равен нулю - система вырождена Во избежание этой ситуации заменим последнее выражение следующим равенством:

P₀+P₁+P₂+P₃+P₄+P₅=1

В заключение вводится вектор искомых величин. Для этого в поле рабочего листа (рис. 5.1.2) определим местоположение вектора, который должен находится несколько ниже системы равенств. Если в окне имеется панель инструментов Math (Математика), щелкнем по кнопке с изображением матрицы. Появится окно Matrix (Матрица), далее - по кнопке с аналогичным изображением или воспользуемся комбинацией клавиш Ctrl+M. В обоих случаях появится диалоговое окно Insert Matrix (Вставить матрицу). В текстовых полях Rows (Строки) и Columns (Столбцы) этого диалогового окна вставляем нужное число строк и столбцов, в нашей задаче - 6 и 1 соответственно.

После щелчка по клавише ОК появится шаблон с метками для ввода искомых параметров (Р₀, Р₁, Р₂, Р₃, Р₄, Р₅). Осуществим эту операцию, подведя курсор или указатель мыши к каждой метке. Затем произведем ввод знака присваивания и имени встроенной функции Find(P₀, P₁, P₂, P₃, P₄, P₅). Введем на рабочем листе четвертый пункт расчета (рис. 5.1.2). Он будет выглядеть так: 4. 4 Результаты решения.

Для получения результатов расчета искомых величин достаточно набрать имя нужного параметра и знак равенства, нажав соответствующую клавишу или щелкнув по кнопке со знаком равенства, расположенной в верхнем левом углу панели инструментов Evalu... (Вычисления).

Анализируя полученные результаты решения в системе Mathcad, можно заметить, что значения для параметров Р₀, Р., Р₂, Р₃, Р₄, Р₅ совпадают с соответствующими значениями, полученными вручную.